확률과 통계의 정의
확률과 통계

통계학의 정의
불확실한 상황에서 데이터에 근거하여 과학적인 의사결정을 도출하기 위한 이론과 방법 체계모집단으로부터 수집된데이터(sample)를 기반으로 모집단의 특성을추론하는 것을 목표로 함
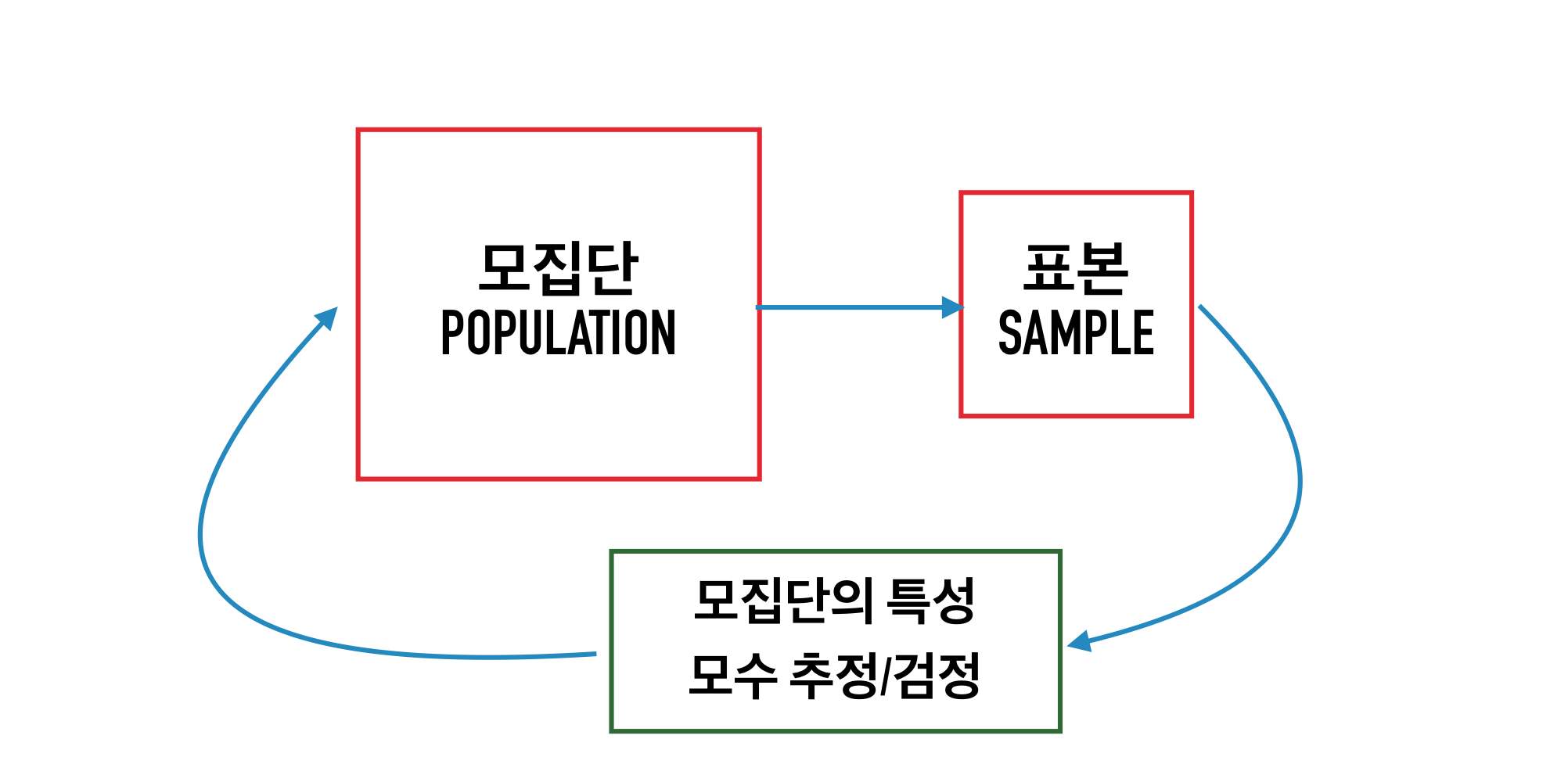
모집단: 통계분석의 대상이 되는 모든 개체들의 집합표본: 모집단으로부터 일정한 규칙에 의해 추출한 부분집합
확률의 개념
모집단에서 특정 사건(event)의 상대도수의 극한
Law of Large Numbers
무수히 많은 시행이 반복되면 상대도수에 의해 계산되는 확률(통계적 확률)이 이론적 확률로 수렴한다.
Sample Space and Events
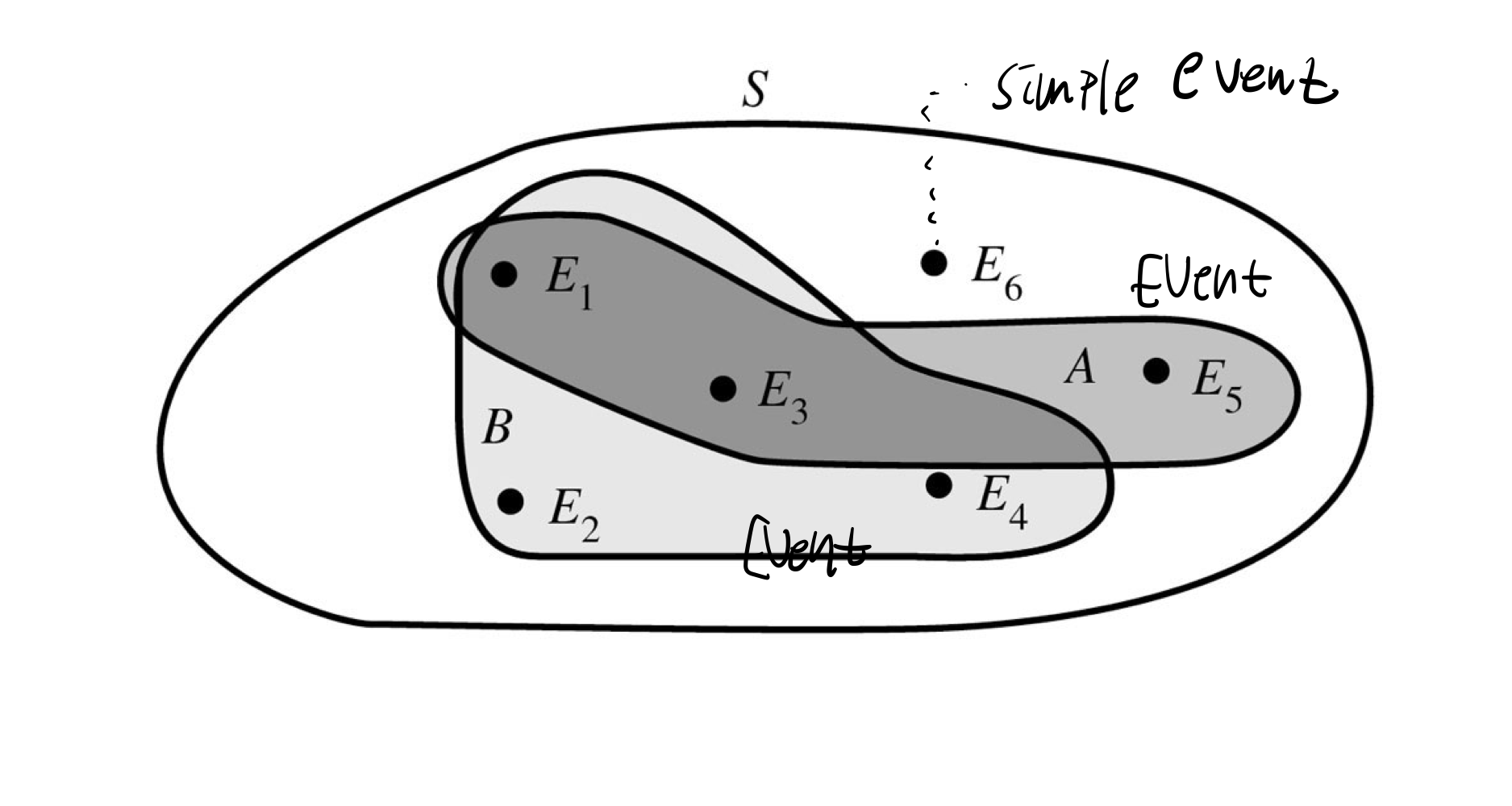
Experiment(확률실험): 동일한 조건에서 독립적으로 반복할 수 있는 실험이나 관측Sample space(표본공간): 모든 simple event의 집합Event(사건): 실험에서 발생하는 결과 (부분 집합)Simple event(단순사건): 원소가 하나인 사건
확률의 정의
- 고전적 확률: 모든 simple event가
동일한 확률을 가질 때 P(A)는 sample space가 n개의 원소로 이루어져 있을 때 k개의 원소를 가지는 event A의 확률 - 통계적 확률: simple event가
동일한 확률을 가지지 않아도 된다.표본의 수가 무한대로 갈 때, 표본의 확률이수렴하는 값
확률의 성질
- 모든x에 대하여 P(x) >= 0
- P(sample space) = 1
- A와 B가 배반사건이면 P(A or B) = P(A) + P(B)
조건부 확률
Event B가 발생했을 때 Event A의 확률 \[P(A|B) = \frac{P(A∩B)}{P(B)}\]
결합확률 (joint probability): P(A∩B)
주변확률 (marginal probability): P(A), P(B), …
Multiplication Law
\[P(A∩B) = P(A|B)P(B)\]
Independent Events
- 두 사건 A와 B가 독립일 때, P(A|B) = P(A), P(B|A) = P(B)
- sample space는 임의의 event와 독립이다.
- 공집합은 임의의 event와 독립이다. (P(∅∩A) = P(∅) * P(A) = 0 * P(A) = 0 = P(∅))
베이즈 정리
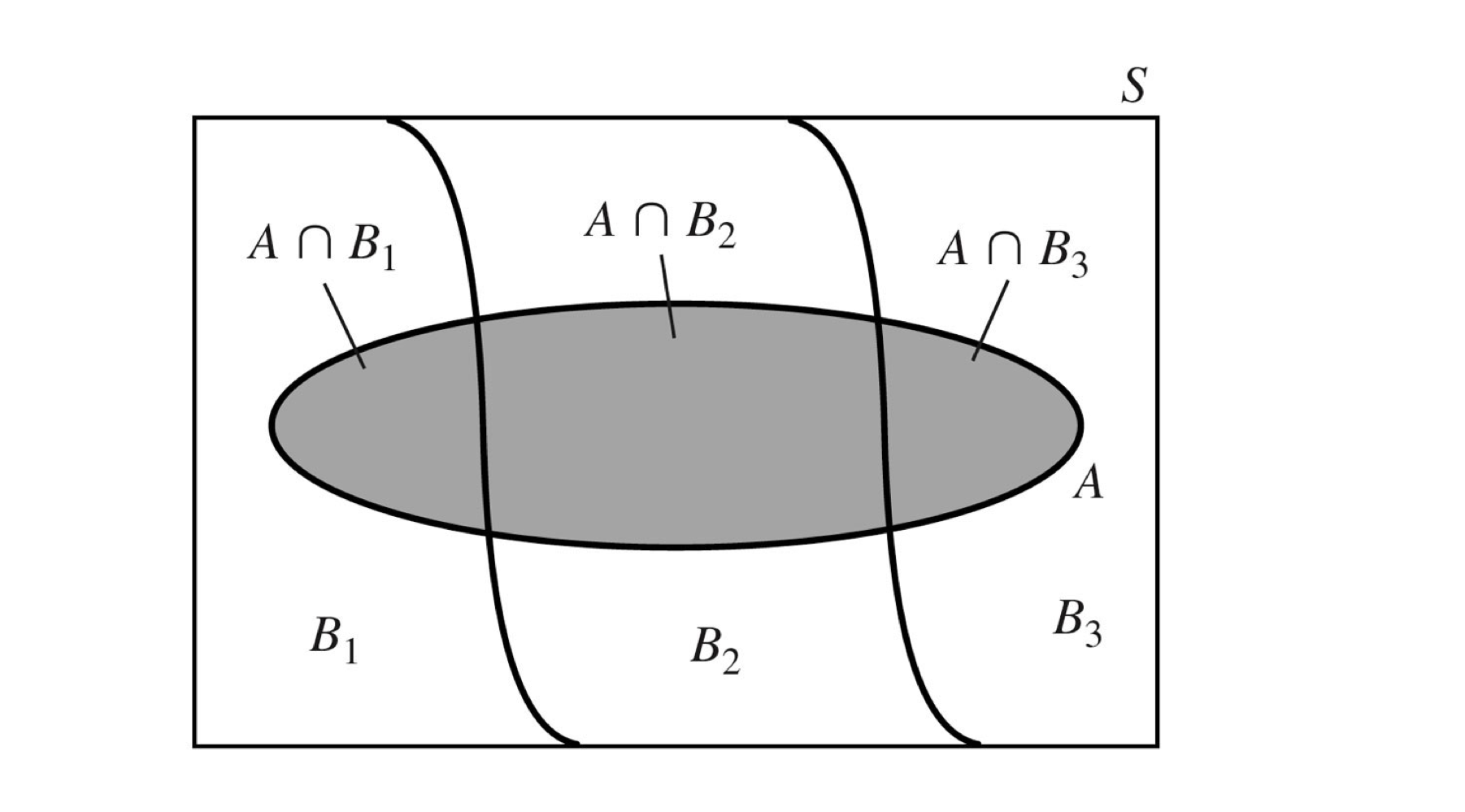
- sample space를 상호 배반인 {B1, B2, …, Bn}으로 분할 (partition)
- \(P(A) = P(A∩B_1) + P(A∩B_2) + ... + P(A∩B_n)\)