배치 생산 및 경제적 주문량 모형

생산시스템관리
공개

2025년 4월 2일

setup과 생산주기

  • setup: 기계를 준비하는데 필요한 것
    • 정확히 하나의 제품을 만드는 경우에도 setup이 필요함
    • 생산하는 양에 관계없이 setup 시간이 일정함
    • sequence dependent setup: 순서에 따라 setup 시간이 달라짐
  • 생산주기(production cycle): setup + 생산의 과정을 반복
    • setup은 아무것도 못하고 시간을 버림

배치 생산과정

  • batch1: 부품 집합을 흐름 단위로 사용
  • 생산 주기: batch size만큼 생산하는 주기
  • 처리능력: \(\frac{batch size}{setup time + (batch size * processing time per unit)}\)
    • batch size가 무한히 커질수록 \(\frac{1}{p}\)로 수렴
    • setuptime이 0이여도 \(\frac{1}{p}\)

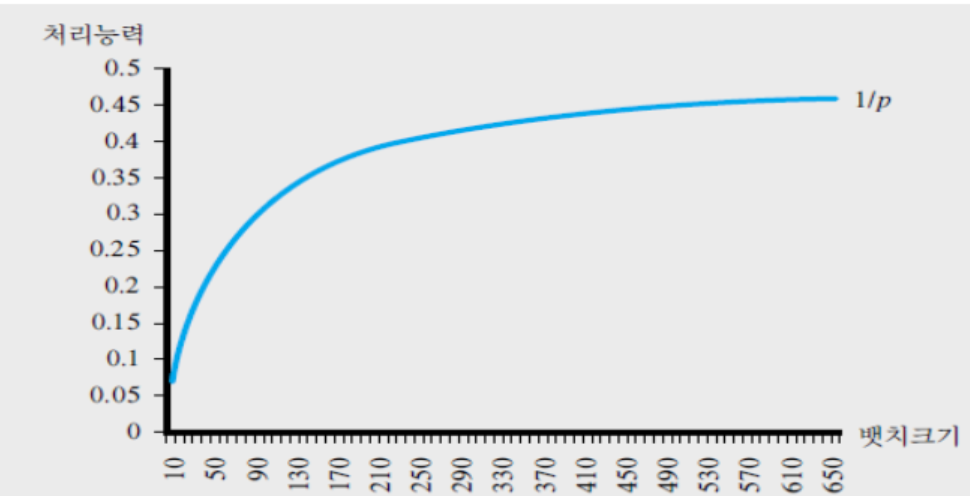
  • batch는 클 수록 좋은가?
    • batch size가 커질수록 처리능력이 증가하지만 재고가 많아짐
    • → 처리능력 제약적 상황에서 bottleneck의 batch size를 늘리고, 수요 제약적 상황에서 non-bottleneck의 batch size를 줄이는게 좋음
    • → \(\frac{B}{S + Bp} = R → B = \frac{SR}{1 - Rp}\)
    • R보다 크면 쓸데없이 제고가 쌓이고, 작으면 capacity가 낮아짐
  • S가 늘어나면 Batch size를 키우고, 낮아지면 Batch size를 줄여도 됨
  • p가 늘어나면 Batch size를 키우고, 낮아지면 Batch size를 줄여도 됨

경제적 주문량 모형

  • 외부 공급자에게 부품을 주문하여 생산 및 배송이 이루어지는 경우
  • 단위시간당 발생하는 비용이 적을수록 좋다

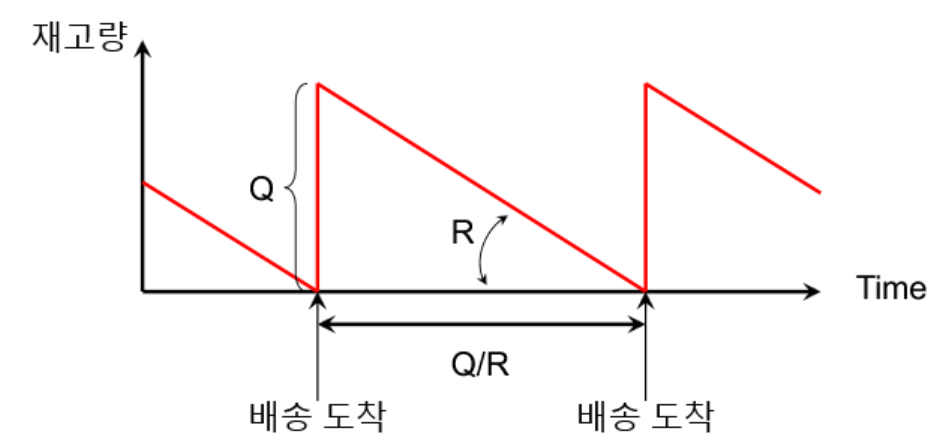
재고량 패턴(재고가 0이 되었을 때 정확히 도착하도록 주문할 수 있다고 가정)
  • Q: 한 번에 주문하는 양
  • R: 수요(기울기)
  • 주문 주기: \(\frac{Q}{R}\)
  • 평균 재고량: \(\frac{Q}{2}\)
  1. 구매비용(purchase cost / variable cost): 단위 시간 당 구매비용은 Q에 영향을 받지 않음
  2. 단위 재고 비용(h)
    • 단위 시간 당 발생하는 재고 비용: \(h\frac{Q}{2}\)
  3. 셋업(주문) 비용 (Fixed cost) (k): 주문량과 무관
    • 단위 시간 당 발생하는 셋업 비용: \(\frac{k}{\frac{Q}{R}}\)

  • 목적 함수: \(C(Q) = \frac{KR}{Q} + \frac{hQ}{2}\)

  • 경제적 주문량(EOQ): \(Q^* = \sqrt{\frac{2KR}{h}}\)

    • K: 주문비용
    • R: 수요량
    • h: 단위 재고비용

  • EOQ만큼 주문할 때 단위 시간당 비용

    • \(C(Q^*) = \sqrt{2KhR}\)

  • 단위당 비용 = \(\frac{C(Q^*)}{R} = \sqrt{\frac{2Kh}{R}}\)

  • 수요가 증가함에 따라 EOQ는 늘어나는데 단위 당 비용은 감소

  • \(\frac{C(Q)}{C(Q^*)} = \frac{1}{2}(\frac{Q^*}{Q} + \frac{Q}{Q^*})\)

  • \(\frac{1}{주문 주기} ≠ 재고 회전율\)

    • 주문 주기는 Q개가 다 없어지는 시간
    • 회전율은 Q/2개의 재고가 다 없어지는 시간

buffer or suffer

  • buffer 제고가 없으면 처리능력이 떨어질 수 있다.
맨 위로

각주

  1. batch 1개는 부품 집합 1 단위 의미↩︎