신경망

deep learning

공개

2025년 3월 18일

신경망이란

퍼셉트론에서 가중치를 자동으로 학습하는 방법이다.
입력층, 은닉층, 출력층으로 구성된다.

앞에서 살펴본 퍼셉트론 함수를 다시 살펴보자.

\[ y = \begin{cases} 0 & (b + w_1x_1 + w_2x_2 ≤ 0) \\ 1 & (b + w_1x_1 + w_2x_2 > 0) \end{cases} \]

이때, \(y = h(b + w_1x_1 + w_2x_2)\)로 표현하면 다음과 같이 표현할 수 있다.

\[ h(x) = \begin{cases} 0 & (x ≤ 0) \\ 1 & (x > 0) \end{cases} \]

이때 \(h(x)\)는 활성화 함수(activation function)라고 한다.

활성화 함수

계단 함수(step function): 앞서 살펴본 함수

import numpy as np

def step_function(x):
    return np.array(x > 0, dtype=int)

print(step_function(np.array([-1.0, 1.0, 2.0])))

[0 1 1]

import matplotlib.pyplot as plt

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()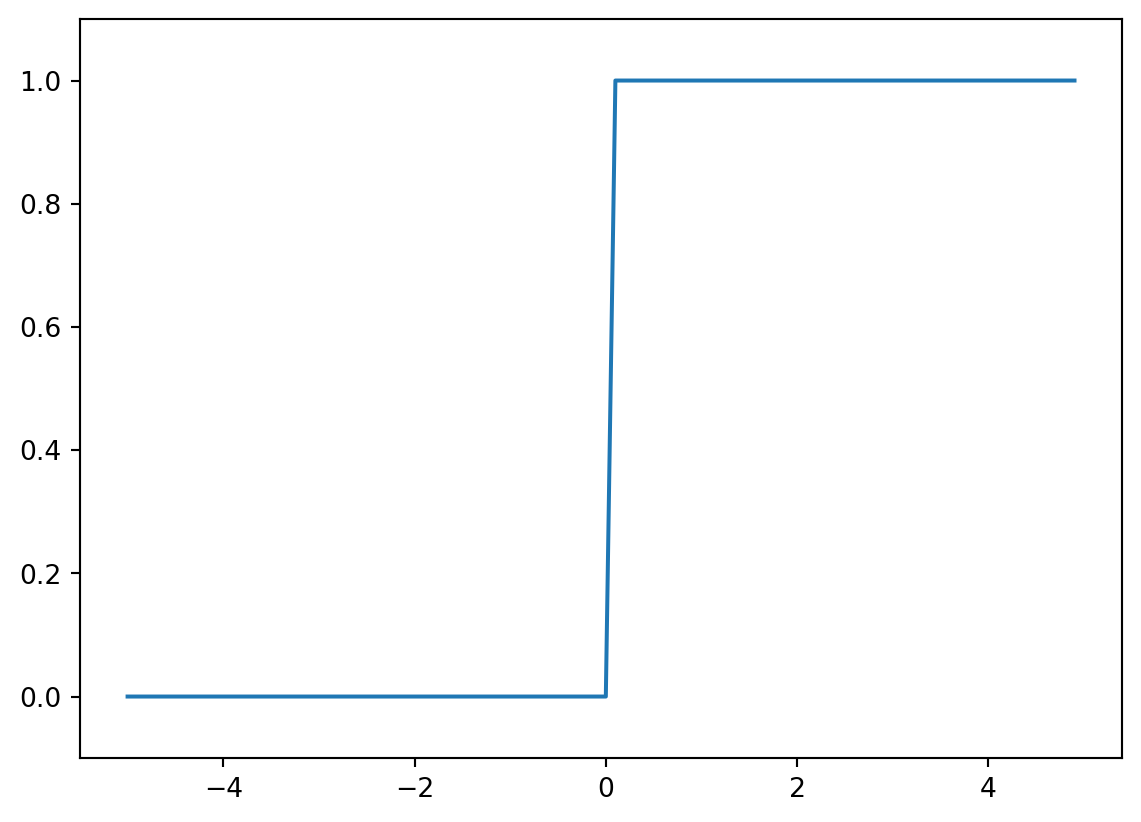

시그모이드 함수: \(h(x) = \frac{1}{1 + \exp(-x)}\)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()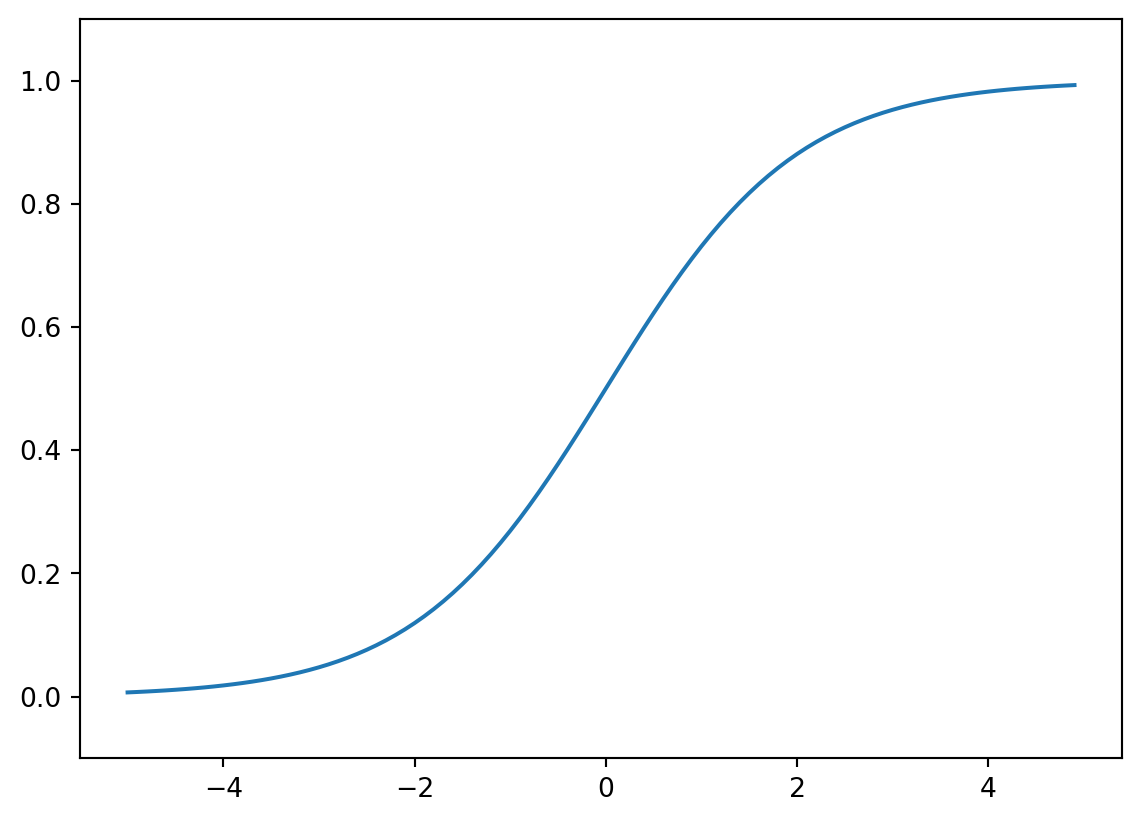

계단 함수와의 차이점
- 시그모이드가 더 부드러움
계단 함수와의 공통점
- 입력이 작을 때는 0에 가깝고, 입력이 커지면 1에 가까워짐
- 입력이 아무리 작거나 커도 출력은 0에서 1 사이
- 비선형 함수 (선형 함수는 은닉층 업싱도 똑같이 구현할 수 있기 때문에 신경망에서 활성화 함수는 반드시 비선형 함수여야 함)
ReLU 함수: \(h(x) = \begin{cases} x & (x > 0) \\ 0 & (x ≤ 0) \end{cases}\)

def relu(x):
    return np.maximum(0, x)

SoftMax 함수: \(y_k = \frac{\exp(a_k)}{\sum_{i=1}^{n} \exp(a_i)}\)

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

softmax 함수는 값이 기하급수적으로 증가하기 때문에 쉽게 overflow가 발생할 수 있음.

따라서 다음과 같이 개선이 필요함

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

sofrmax 함수 출력의 총합은 1이고, 개별 출력은 0에서 1 사이이다.

따라서 softmax 함수의 출력을 확률로 해석할 수 있다.

추론 단계에서 출력층의 softmax 함수는 생략하는 것이 일반적이다.

3층 신경망 구성

입력층에서 1층으로 신호 전달

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])

A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)

print(A1)
print(Z1)

[0.3 0.7 1.1]
[0.57444252 0.66818777 0.75026011]

1층에서 2층으로 신호 전달

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

print(A2)
print(Z2)

[0.51615984 1.21402696]
[0.62624937 0.7710107 ]

2층에서 출력층으로 신호 전달

def identity_function(x):
    return x

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)

출력층의 활성화 함수는 보통 풀고자 하는 문제의 성질에 맞게 정함

회귀: 항등 함수
2클래스 분류: 시그모이드 함수
다중 클래스 분류: 소프트맥스 함수

맨 위로