Regression Analysis

확률과 통계
공개

2025년 5월 13일

통계학습 및 회귀분석

  • 통계 학습: 관측된 X, Y 데이터로부터 X와 Y의 관계를 추정하는 것
  • \(Y = f(X) + ϵ\)
  • 선형 회귀 모형: 독립변수와 종속변수 사이의 관계를 선형으로 가정하는 모형

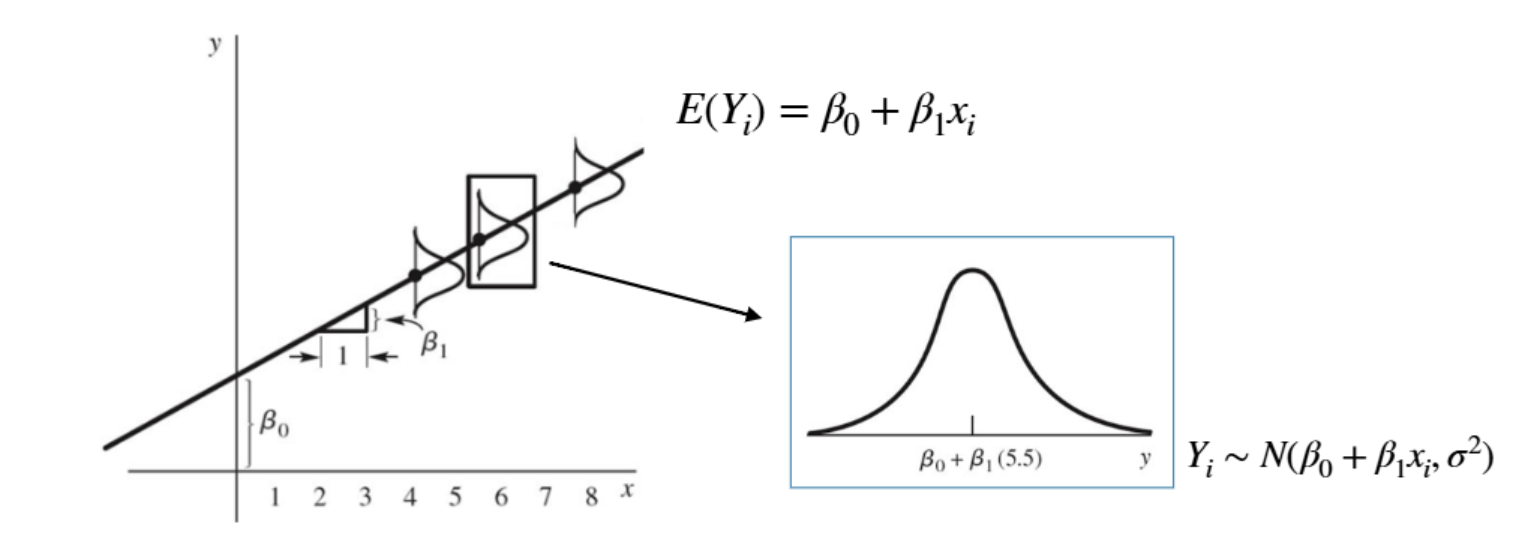
단순 선형회귀모형

  • \(Y_i = β_0 + β_1x_i + ϵ_i\)
  • \(β_0 + β_1x_i\): 회귀 계수, 선형 모형으로 설명 가능한 부분
  • \(ϵ_i\): 오차항, 선형 모형으로 설명할 수 없는 부분
    • \(ϵ_i ~^{iid} N(0, σ^2) → Y_i ~ N(β_0 + β_1x_i, σ^2)\)

\(Y_i\)는 iid는 아니다.

회귀계수의 추정

  • 최소 제곱법: 잔차 제곱합을 최소화하는 방법
    • → \(SS_E\)를 \(\hat{β}_0, \hat{β}_1\)에 대해 미분하여 0으로 만드는 \(\hat{β}_0, \hat{β}_1\).
    • \(β_0 = \bar{Y} - β_1\bar{X}\), \(β_1 = \frac{S_{XY}}{S_{XX}}\)
    • \(Σ_{i=1}^n e_i = 0\), \(Σ_{i=1}^n x_ie_i = 0\)
  • 회귀계수 추정 시에는 오차항의 분포에 대한 가정이 사용되지 않는다.
  • 독립변수의 단위가 달라지면, 회귀계수의 단위도 달라진다. (설명력은 동일하다)
  • 표본의 수가 늘어나면, \(β_1\)은 수렴한다.

회귀모형의 적합성

  • \(SS_T = S_{YY}\)
  • \(SS_R = \frac{S_{XY}^2}{S_{XX}}\)
  • \(SS_E = SS_T - SS_R\)

모형 적합성 - 결정계수: \(R^2 = \frac{SS_R}{SS_T} = 1 - \frac{SS_E}{SS_T}\) - \(R^2\)는 모형이 종속변수의 변동을 얼마나 설명하는지 나타내는 지표 - 오차를 최소화하면 \(R^2\) 값 증가 - \(\frac{S_{XY}^2}{S_{XX}S_{YY}} = r(X, Y)^2\)

회귀계수에 대한 추론

  • \(H_0: β_1 = 0\) (독립변수와 종속변수 사이에 관계가 없다)
  • \(β_1\)은 불편추정량, 정규분포를 따른다.
  • \(Var(β_1) = \frac{MS_E}{S_{XX}}\)

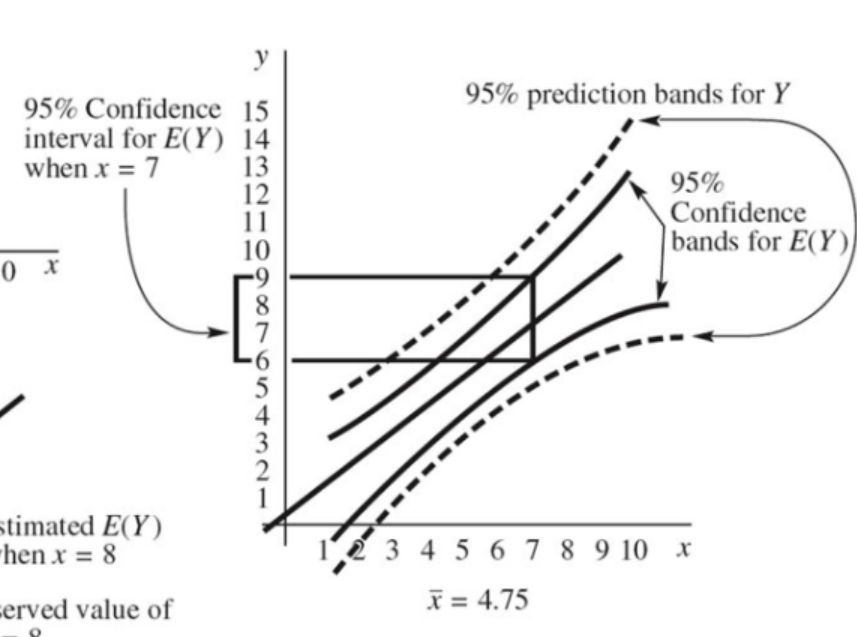
종속변수의 신뢰구간과 예측구간

  • \(\hat{Y_0} = \hat{β}_0 + \hat{β}_1x_0\)
  • \(Var(\hat{Y_0}) = MS_E(\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{XX}})\)
  • 예측 구간에서의 오차의 분산은 \(MS_E(1 + \frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{XX}})\)

종속변수의 예측 / 신뢰구간은 평균일 때 가장 짧음

잔차 분석

  1. 불편성
  2. 정규성
  3. 독립성
  4. 등분산성

오차의 추정치인 잔차를 통해 위의 가정을 검증할 수 있다.

  • 선형성: 잔차그림이 특정 패턴을 보이지 않는다.
    • 만족하지 않을 경우: 독립변수 변환
  • 등분산성: 잔차그림의 분산이 일정하다.
    • 만족하지 않는 경우: 반응치를 log 변환할 수 있다.
  • 독립성: 시계열 데이터의 경우, 자기상관을 고려해야 한다.
  • 정규성: normal Q-Q plot / shapiro-wilk test
    • 만족하지 않는 경우: 반응치를 log 변환할 수 있다.
맨 위로