벡터와 공간

what is vector

vector는 크기(magnitude)와 방향(direction)을 가지고 있고, 2, 3, 4 차원 너머를 수학적으로 표현할 수 있다.

vector의 수학적 표현

vector는 ordered list인 tuple 형태로 표현할 수 있다.

\[ \vec{v} = \begin{bmatrix} 3 \\ 4 \end{bmatrix} \]

domain과 dimension에 따라 vector는 다음과 같이 표현할 수 있다.

\[ \vec{v} ∈ R^2 \]

• 1차원: \(R^1\)
• 2차원: \(R^2\)
• 3차원: \(R^3\)
• n차원: \(R^n\)

vector의 합

vector의 합은 각 성분별로 더한 결과를 반환한다.

기하학적 의미

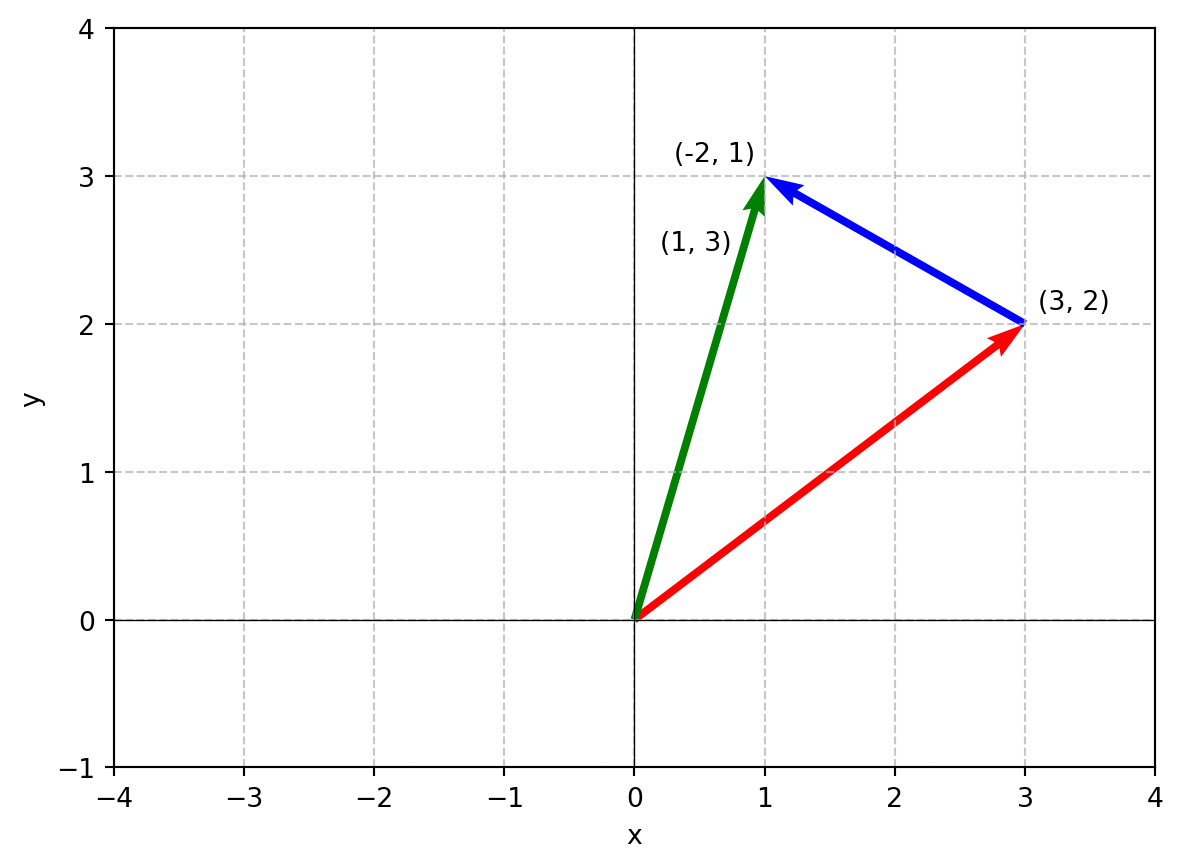
\[ \begin{bmatrix} 3 \\ 2 \end{bmatrix} + \begin{bmatrix} -2 \\ 1 \end{bmatrix} \]

위의 수식을 좌표평면에 나타나면 다음과 같다.

끝점을 다 더한 좌표와 시작 점을 연결한 벡터인 초록색 화살표가 두 벡터의 합이 된다.

vector의 scalar 곱

vector에 scalar, 즉 숫자 하나를 곱하면 무슨 일이 생길까?

\[ 2 * \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} \] \[ -2 * \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} -4 \\ -2 \end{bmatrix} \]

vector의 차

vector의 차는 각 성분별로 뺀 결과를 반환한다.

기하학적으로는 두 벡터의 끝점을 연결한 벡터가 된다.

\(\vec{x} - \vec{y}\)는 y에서 x를 연결한 벡터가 된다.

\(\vec{y} - \vec{x}\)는 x에서 y를 연결한 벡터가 된다.

단위 벡터

\[ \vec{v} = \begin{bmatrix} 3 \\ 4 \end{bmatrix} \]

위의 벡터를 단위 벡터의 합으로 만들면 다음과 같다.

\[ \hat{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \hat{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \]

\[ \vec{v} = 3\hat{i} + 4\hat{j} \]

Scalar 배를 한 기저 벡터끼리 더하면 모든 2차원 좌표를 표현할 수 있다.