프로세스 성과에 미치는 변동성의 영향: 대기시간 문제
생산시스템관리

Intro
- 지금까지는 변동성을 고려하지 않았지만 프로세스 성과 평가에 중요한 영향을 미친다.
- 변동성이 대기시간에 미치는 영향을 살펴본다.
Example
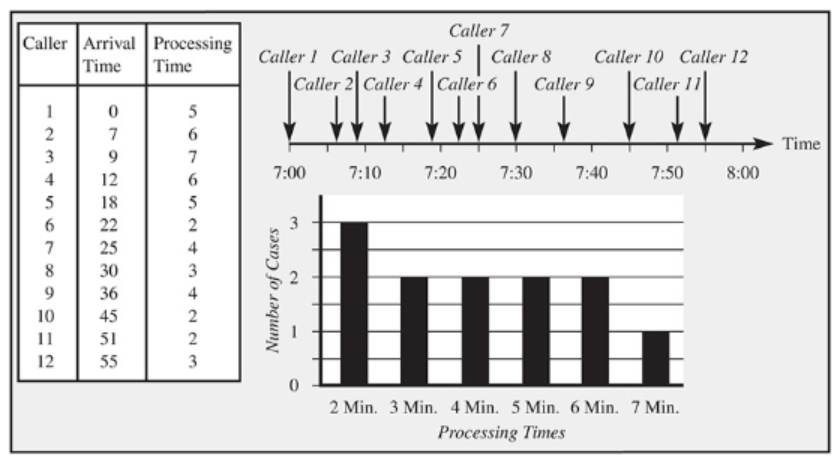
- 변동성
- 불규칙한 도착 간격
- 서비스 시간의 변동성
- 영향: 재고, 대기시간, 산출 손실
- IU가 100 이하여도 대기가 발생할 수 있음
변동성의 원인
- 흐름단위의 input (\(CV_a\))
- random arrival
- incoming quality
- product mix
- processing time의 변동성 (\(CV_p\))
- 그냥 내재적인 변동성
- 숙련도 (일을 못해서 오래걸림)
- 품질 (재작업)
- 자원의 무작위적 가용성
- 자원 고장
- 작업자 출근 안함
- setup time
- 복수의 흐름단위가 무작위적 경로결정
- 경로의 변동성
- 변동성의 측정: \(\frac{표준편차}{평균}\)
대기시간 예측 (단일 자원)
가정
- 내재활용률은 100% 미만
- if D > C, 대기 - 처리능력 부족 (+ 변동성)
- if D < C, 대기 - 변동성
- 안정적 도착: 평균 고객 수가 시점에 의존하지 않고, 길이에만 의존함
- 만약 프로세스가 안정적이지 않다면 더 짧은 시간간격으로 나누어 접근
- 지수분포를 따르는 도착간격
- \(CV_a = 1\)
- 비기억 특성
변수
- a: 평균 도착 간격 (줄 기준)
- p: 평균 서비스 시간
- \(CV_a\): 도착간격의 변동계수
- \(CV_p\): 서비스 시간의 변동계수
- \(T_q\): 대기 시간
- \(I_q\): 대기열의 재고
- \(I_p\): 서비스 중 재고
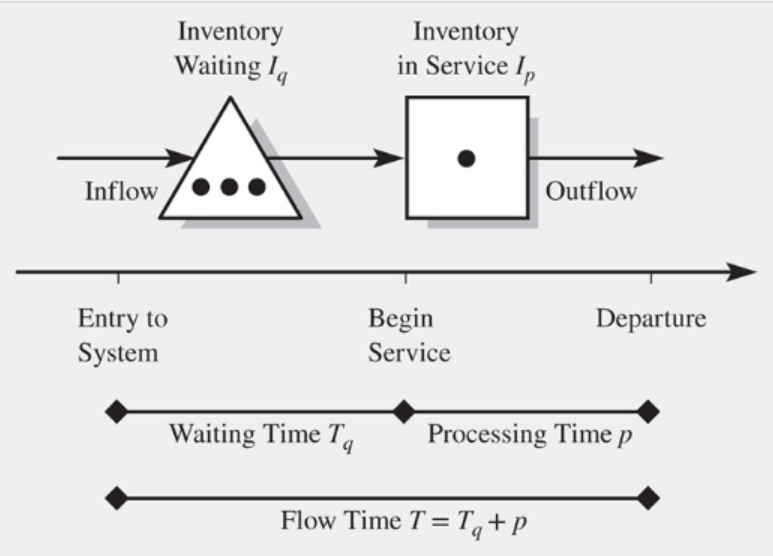
공식
- capacity: \(\frac{1}{p}\)
- flow rate = demand(수요 제약적 상황을 가정하니까): \(\frac{1}{a}\)
- utilization: \(\frac{p}{a}\)
- T: \(T_q\) + p
- \(I_p\): (1 - u) * 0 + u * 1 = u
- I = \(I_q\) + \(I_p\) = \(I_q\) + utilization
- \(T_q = p * \frac{u}{1-u} * \frac{CV_a^2 + CV_p^2}{2}\)
- 도착 간격이 지수분포를 따르지 않는 경우 근사치만을 제공
- \(I_q = \frac{1}{a} * T_q = \frac{T_q}{a}\)
대기시간 예측 (복수 자원)
- capacity: \(\frac{m}{p}\)
- flow rate: \(\frac{p}{am}\)
- \(I = I_q + I_p = I_q + mu\)
- \(T_q = \frac{p}{m} * \frac{u^{\sqrt{2(m+1)} - 1}}{1-u} * \frac{CV_a^2 + CV_p^2}{2}\)
- 근사치만을 제공
- service level: \(P(T_q ≤ TWT)\)
풀링
- 대기할 수 있는 방법은 여러가지가 있다
- 대기시간을 줄일 수 있는 방법에 사람을 많이 뽑는것 외에 다른 고려 요소
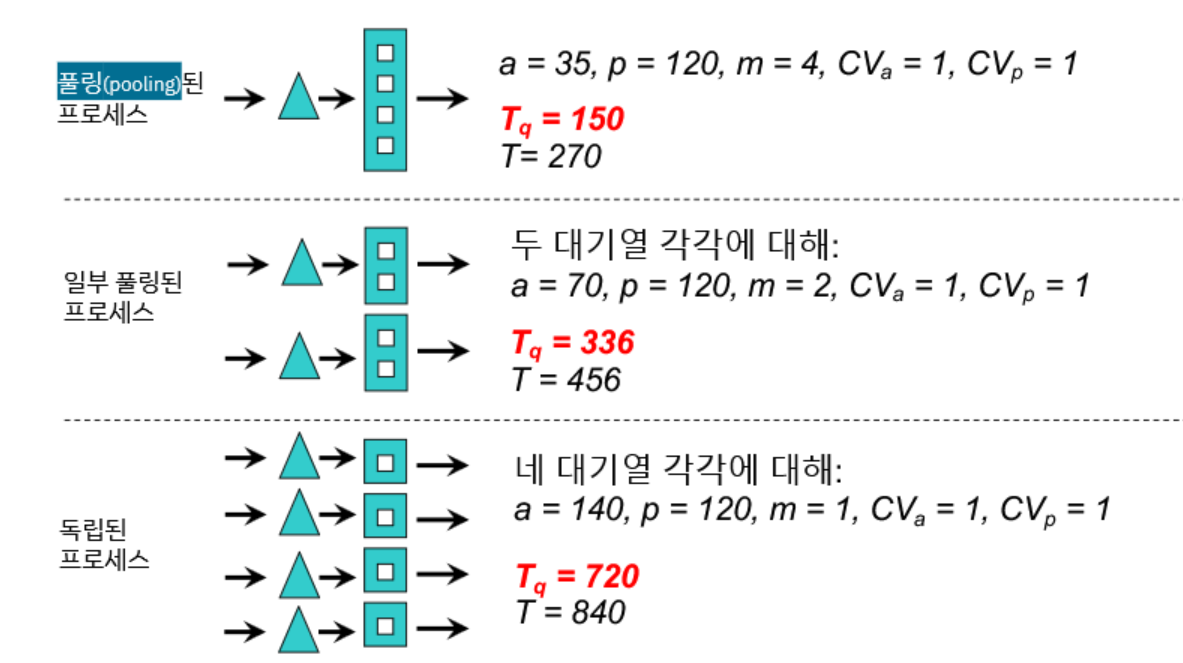
풀링의 효과
풀링되는 시스템이 서로 완전히 독립
다양한 input을 처리할 수 있어야 함.
→ 대기시간, 대기 인원 감소