분류

data mining
공개

2025년 5월 5일

K-NN

  • 새로운 데이터 포인트에 대해 k개의 가장 가까운 이웃을 찾고, 그 이웃들의 클래스를 투표하여 다수결로 분류한다.

의사결정 트리

불순도가 가장 낮은(한쪽의 class가 더 많은) leaves를 root에 두고, 그 다음 불순도가 낮은 leaf를 그 아래에 두는 방식으로 트리를 구성한다. leaf 노드의 과반수가 같은 클래스를 가지면 그 클래스를 리턴한다. overfit을 방지하기 위해 pruning을 하거나 max depth를 설정한다.

  • good split: 불순도가 낮고, 분할된 각 leave의 비율이 비슷한 경우

과정

  1. 루트 노드에서 시작전체 데이터셋을 기준으로 시작하여 가장 좋은 분할속성(feature)을 선택
  2. 분할 기준 평가각 속성에 대해 데이터를 분할했을 때의 분할 평가함수 적용
    • gini index
      • gini: \(1 - \sum_{i=1}^{c} p_i^2\).
      • 목표: 최소화
      • 제일 좋은게 0
      • 제일 안좋은게 0.5
    • misclassification error
      • error: \(1 - \max(p_i)\)
      • 목표: 최소화
      • 제일 좋은게 0
      • 제일 안좋은게 0.5
    • entropy: 유용하지 못한 정보를 포함하고 있는 정도.
      • entropy: \(-\sum_{i=1}^{c} p_i \log_2(p_i)\)
      • 목표: 최소화
      • 제일 좋은게 0
      • 제일 안좋은게 1
    • information gain: 어떤 속성을 기준으로 분할했을 때, 얻을 수 있는 불확실성의 감소량
      • 부모의 엔트로피 - 자식의 엔트로피 가중평균
      • 목표: 최대화
      • 단점: 고유한 값을 많이 갖는 변수를 선호하는 경향이 있음
      • 알고리즘: ID3, C4.5
    • gain ratio: information gain의 단점을 보완한 방법
      • gain ratio: \(\frac{information\ gain}{entropy}\)
      • 분기의 갯수와 각 분기의 크기를 함께 고려
      • 목표: 최대화
      • 단점: entropy가 낮은 것을 선택하는 경향이 있음
        • → 평균이 넘는 entorpy만 선택해서 gain ratio를 계산
      • 알고리즘: C4.5
  3. 최적의 분할 선택 평가된 기준 중 가장 순도가 높은 점수를 갖는 속성을 선택 (greedy)
  4. 재귀적으로 하위 노드 분할. 분할된 하위 데이터에 대해 위의 과정을 반복
  5. 종료 조건 만족 시 정지
  6. 가지치기 수행

Algorithm

  1. CART
    • 분할 기준
      • 분류: gini index
      • 회귀: MSE
    • 모든 분할에서 이진 트리로 분할
    • 사후 가지치기
      • 비용 복잡도 가지치기: \(Total SSR + α(leaf size)\)이 제일 작은 트리 선택
      • α는 cross validation으로 결정

평가

  • confusion matrix

    • TP, TN, FP, FN

  • accuracy: \(\frac{TP + TN}{TP + TN + FP + FN}\)

  • precision(정밀도): true로 예측한 것 중 실제 true인 것의 비율

    • \(\frac{TP}{TP + FP}\)

  • recall(민감도, 재현율): 실제 true인 것 중 true로 예측한 것의 비율

    • \(\frac{TP}{TP + FN}\)

  • F1 score: \(2 \cdot \frac{precision \cdot recall}{precision + recall}\)

  • macro 평균: 그냥 각 클래스의 score를 평균

  • weighted 평균: 가중 평균

  • micro 평균: 전체 TP, TN, FP, FN을 합쳐서 계산

  • ROC curve: y축: TPR(민감도), x축: FPR(1 - 특이도)

    • AUC: ROC curve 아래 면적
      • 1에 가까울수록 좋은 모델
      • 0.5는 랜덤 추측과 같음

  • (1,1): 무작위 추측과 동일. 모든 샘플을 무조건 양성으로 예측

  • (0,0): 모든 샘플을 무조건 음성으로 예측

  • (1,0): 완벽한 모델

  • (0,1): 반대로 예측하는 모델

learning curve

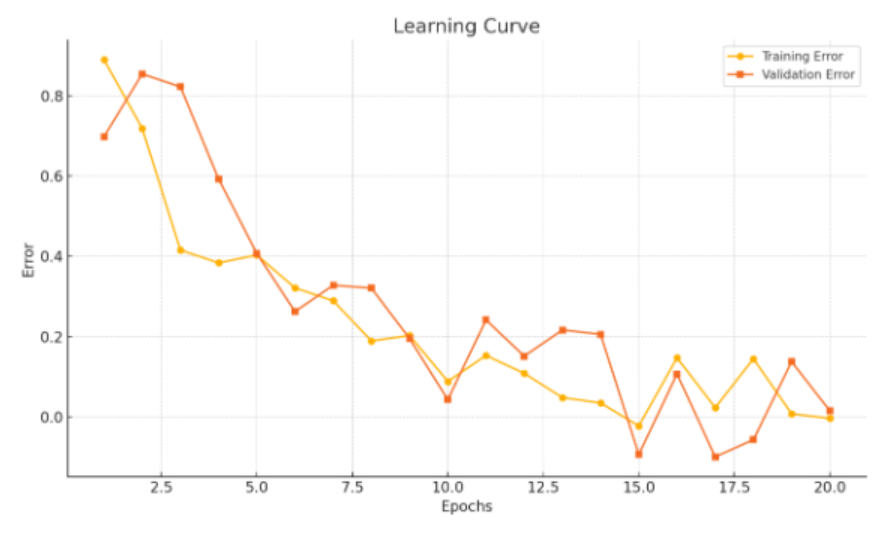
  • sample 수가 적으면 정확도와 신뢰 구간에 부정적 영향을 미침
  • test set에 대한 오류가 증가하는 구간(cross 되는 구간)은 과적합 구간. 여기서 stop
맨 위로