시험 범위
Data Structure
학부 정리

트리
- 차수, 노드의 갯수, 높이 물어봄
- 특정 노드의 부모 / 조상 노드, 단말 노드 수
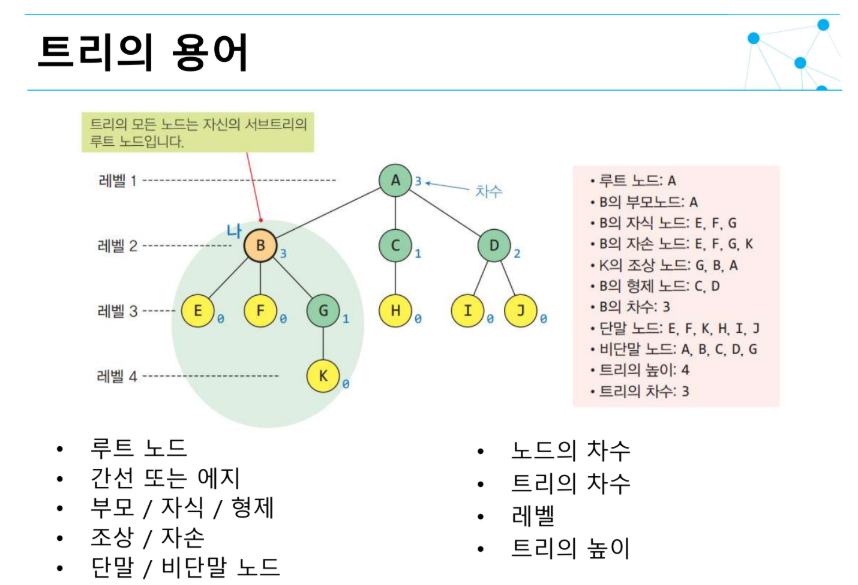
- 트리의 차수: 트리의 최대 차수
- 전위, 중위, 후위 순회 무조건 냄
- 전위 / 후위 중 하나의 결과와 중위순위를 통해 원래 트리 추측하는 문제
- 전위의 맨 앞이랑 후위의 맨 뒤가 루트 노드
- 루트 노드를 알면 중위 순회에서 루트 노드 기준으로 왼쪽 서브트리와 오른쪽 서브트리로 나눌 수 있음
- 트리를 주고 나서 전위 / 중위 / 후위 결과를 기술하라
- 레벨 순위 안냄
힙트리 (15~20)
- 삽입
def insert(self, n):
self.heap.append(n)
i = self.size()
while (i != 1 and n > self.Parent(i)):
self.heap[i] = self.Parent(i)
i = i // 2
self.heap[i] = n- 삭제
def delete(self):
parent = 1
child = 2
if not self.is_empty():
hroot = self.heap[1]
last = self.heap[self.size()]
while child <= self.size():
if (child < self.size() and self.left(parent) < self.right(parent)):
child += 1
if last >= self.heap[child]:
break;
self.heap[parent] = self.heap[child]
parent = child
child = child * 2
self.heap[parent] = last
self.heap.pop(-1)
return hroot상향식 힙 만들기
class Bheap:
def __init__(self, a):
self.a = a
self.N = len(a) - 1
def create_heap(self, k):
for i in range(N // 2, 0, -1):
self.downheap(i)
def insert(self, k):
self.a.append(k)
self.N += 1
self.upheap(self.N)
def delete_min(self):
if self.N == 0:
return None
minimum = self.a[1]
self.a[1], self.a[-1] = self.a[-1], self.a[1]
del self.a[-1]
self.downheap(1)
return minimum
def upheap(self, i):
while i > 1 and self.a[i][0] < self.a[i // 2][0]:
self.a[i], self.a[i // 2] = self.a[i // 2], self.a[i]
i = i // 2
def downheap(self, i):
while i * 2 <= self.N:
k = i * 2
if k < self.N and self.a[k][0] > self.a[k + 1][0]:
k = k+1
if self.a[i][0] < self.a[k][0]:
break
self.a[i], self.a[k] = self.a[k], self.a[i]
i = k삽입, 삭제: O(logN)
이진 탐색 트리 (15~20)
- 이진 탐색 트리
- key 값을 10개정도 쭉 주고 나서 이진 탐색트리로 구현하라
- 이진 탐색 트리를 주고 나서, 노드 삭제 후 최종 이진 탐색 트리 기술하라
연습 문제: BST 빈칸 채우기 (고급)
아래 BST 클래스의 메소드들을 완성해보세요:
class Node:
def __init__(self, key, value, left=None, right=None):
self.key = key
self.value = value
self.left = left
self.right = right
class BST:
def __init__(self):
self.root = None
def get(self, k):
return self.get_item(self.root, k)
def get_item(self, i, k):
if i == None:
return None
if k < i.key:
return self.get_item(i.left, k)
if i.key < k:
return self.get_item(i.right, k)
return i.value
def put(self, k, val):
self.root = self.put_item(self.root, k, val)
def put_item(self, i, k, val):
if self.root == None:
return Node(k, val)
if k < i.key:
self.left = self.put_item(self,left, k, val)
elif i.key < k:
self.right = self.put_item(self.right, k, val)
else:
i.val = val
return i
def min(self):
if self.root == None:
return None
return self.min_item(self.root)
def min_item(self, i):
if i.left == None:
return i
return self.min_item(i.left)
def del_minimum(self):
if self.root == None:
return None
return self.del_min(self.root)
def del_min(self, i):
if i.left == None:
return i.right
i.left = del_min(self.left)
return i
def del(self, k):
if self.root == None:
return None
return self.del_item(self.root, k)
def del_item(i, k):
if k < i.key:
i.left = self.del_item(i.left, k)
elif i.key < k:
i.right = self.del_item(i.right, k)
else:
if i.right == None:
return i.left
if i.left == None:
return i.right
target = i
i = self.min_item(target.right)
i.left = target.left
i.right = self.del_min(target.right)
return i- AVL 안냄
그래프
- 그래프 차수: 정점에 인접한 정점의 수
- kruscal, prim(둘 중 하나) 30~40
kruscal
weights = [(0, 1, 9), (0, 2, 10)]
weights.sort(key = lambda t: t[2])
mst = []
N = 7
p = [] * N
def find(a):
if a != p[a]:
p[a] = find(p[a])
return p[a]
def union(u, v):
root1 = find(u)
root2 = find(v)
p[root1] = root2
e = 0
cost = 0
while True:
if e == N - 1:
break
u, v, wt = weights.pop(0)
if find(u) != find(v):
union(u, v)
mst.append((u, v))
cost += wt
e += 1
print(cost)
print(mst)O(MlogN)
prim
import sys
N=8
s=0
g = [None] * N
g[0] = [(1, 1), (3, 2)]
g[1] = []
visited = [False] * N
D = [sys.maxsize] * N
D[s] = 0
previous = [None] * N
previous[s] = s
for k in range(N):
m = -1
min_val = sys.maxsize
for j in range(N):
if not visited[j] and D[j] < min_val:
m = j
min_val = D[j]
visited[m] = True
for v, wt in list(g[m]):
if not visited[v]:
if wt < D[v]:
D[v] = wt
previous[v] = m그래프가 희소그래프이고, 이진힙 쓰면 O(NlogN) 아니면 O(N^2)
- 다익스트라(필수)
import sys
N=8
s=0
g = [None] * N
g[0] = [(1, 1), (3, 2)]
g[1] = []
visited = [False] * N
D = [sys.maxsize] * N
D[s] = 0
previous = [None] * N
previous[s] = s
for k in range(N):
m = -1
min_val = sys.maxsize
for j in range(N):
if not visited[j] and D[j] < min_val:
min_val = D[j]
m = j
visted[m] = True
for v, wt in list(g[m]):
if not visted[v]:
if D[m] + wt < D[v]:
D[v] = D[m] + wt
previous[v] = mO(N^2)
- BFS, DFS (5~10)
- BFS
adj_list = [[2, 1], [3, 0]]
N = len(adj_list)
visited = [None] * N
def bfs(i):
queue = []
visited[i] = True
queue.append(i)
while len(queue) != 0:
v = queue.pop(0)
print(v, ' ', end='')
for i in adj[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
for i in range(N):
if not visited[i]:
bfs(i)O(N + M)
- DFS
adj_list = [[2, 1], [3, 0]]
N = len(adj_list)
visited = [None] * N
def dfs(v):
visited[v] = True
print(v, ' ', end='')
for i in adj_list[v]:
if not visited[i]:
dfs(i)
for i in range(N):
if not visited[i]:
dfs(i)O(N + M)