확률과 통계 R 실습 과제

One-way ANOVA

a

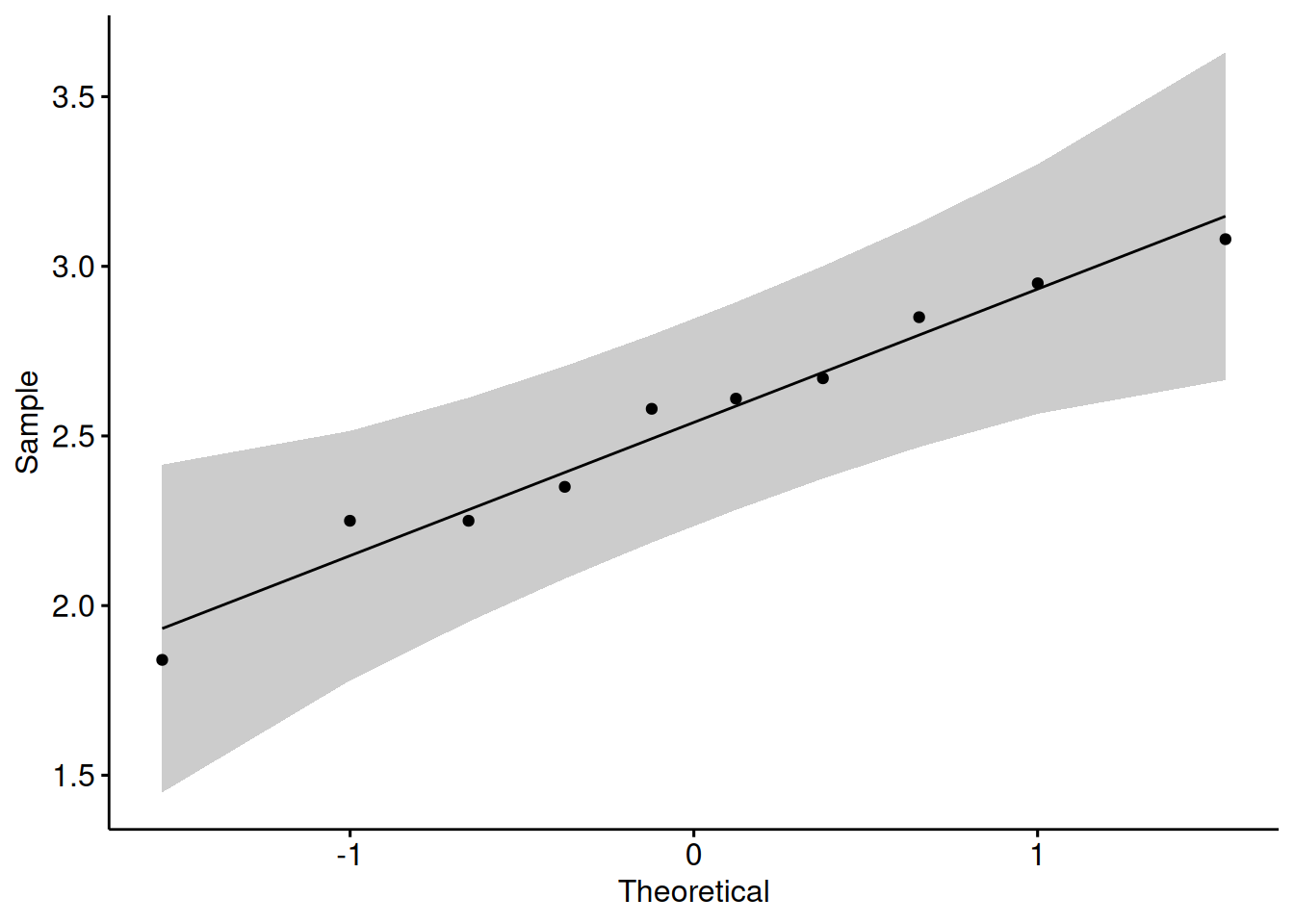
val1 <- c(1.84, 2.67, 2.61, 2.95, 2.25, 2.35, 2.85, 2.58, 3.08, 2.25)
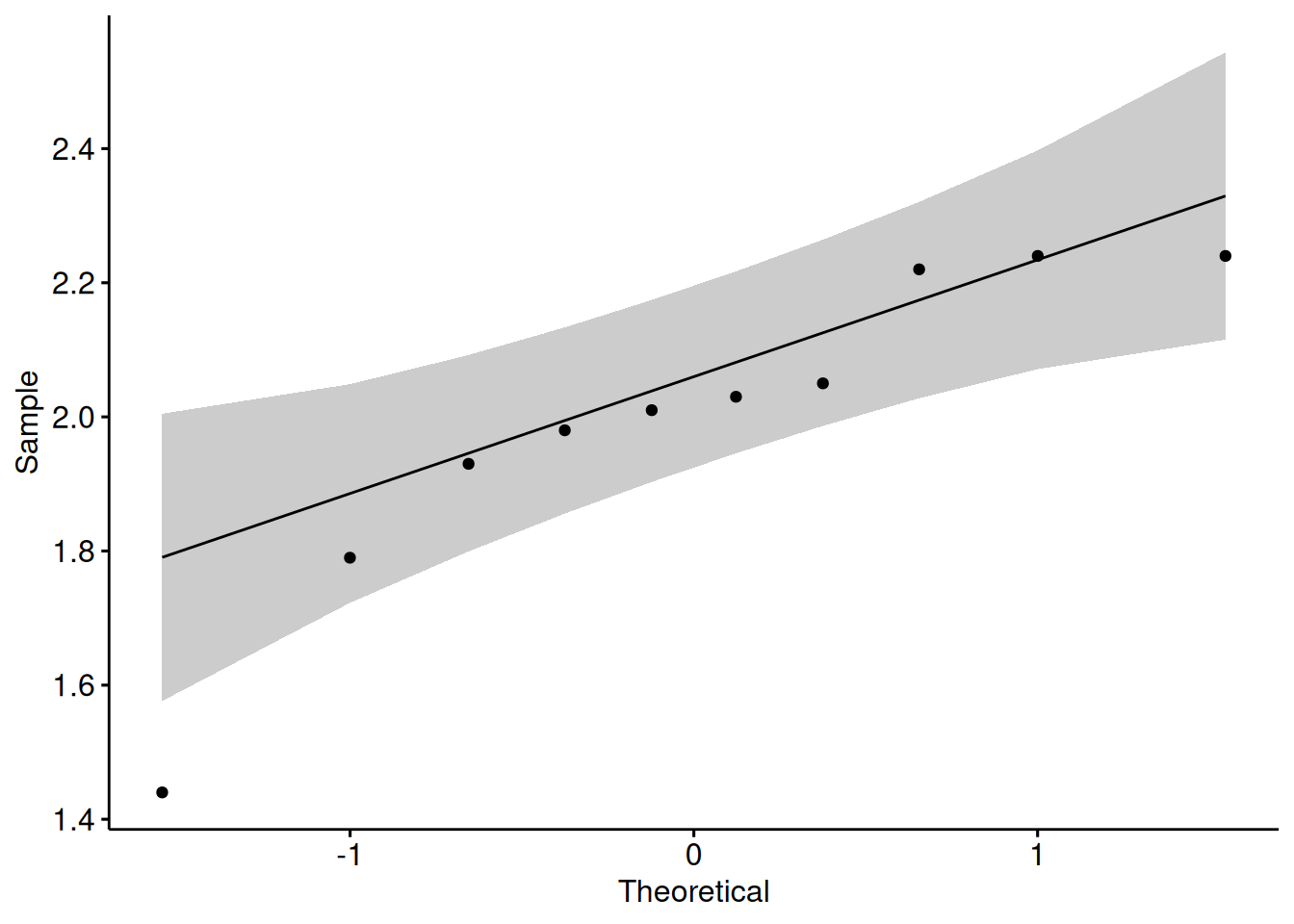
val2 <- c(1.79, 1.98, 2.01, 1.93, 2.24, 2.03, 2.22, 1.44, 2.24, 2.05)
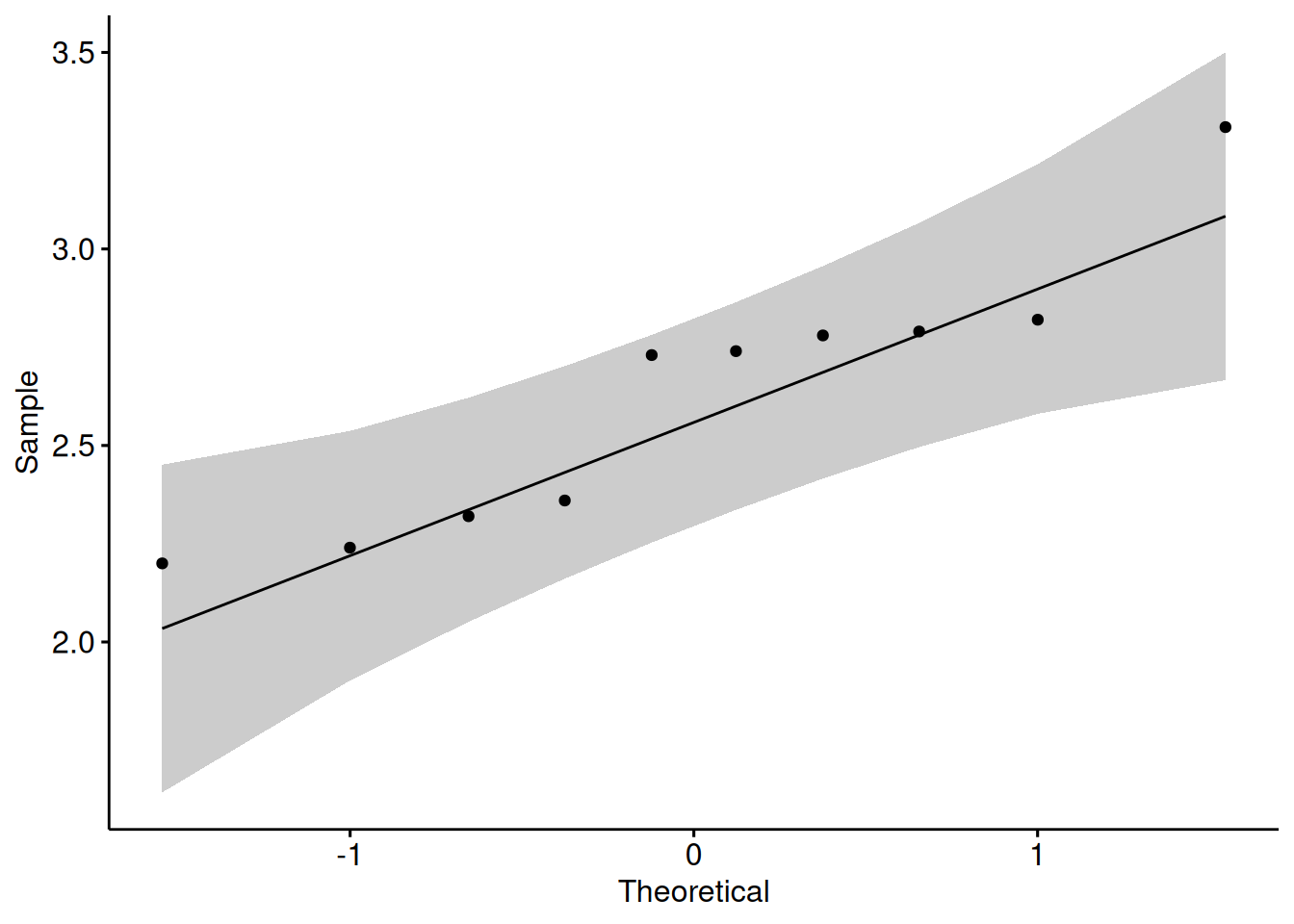
val3 <- c(3.31, 2.24, 2.74, 2.36, 2.79, 2.20, 2.32, 2.82, 2.73, 2.78)
df <- data.frame(
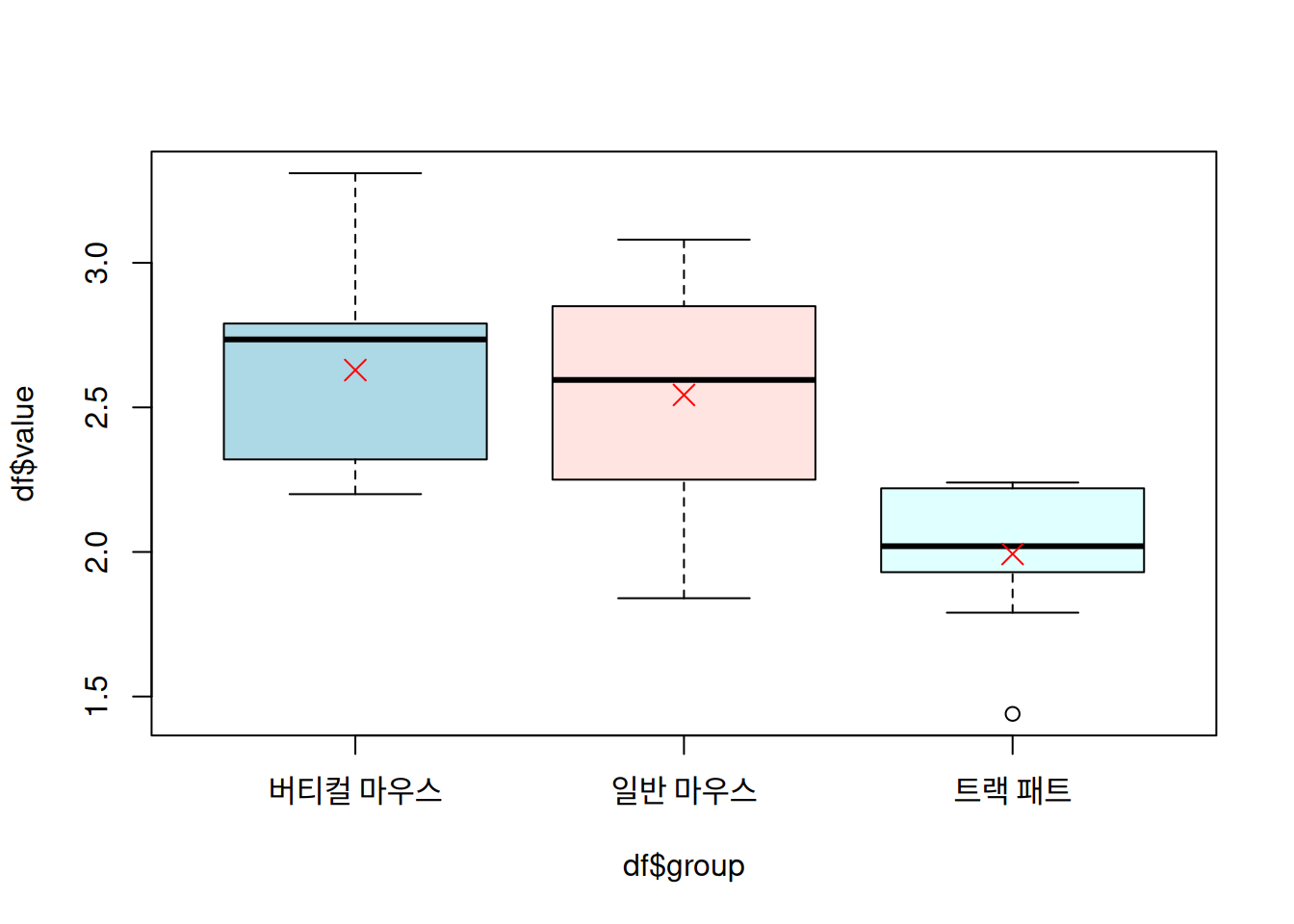
  group = c(rep("일반 마우스", 10), rep("트랙 패트", 10), rep("버티컬 마우스", 10)),
  finger = c('왼중지', '왼검지', '오른약지', '왼약지', '왼엄지', '오른약지', '오른새끼', '오른엄지', '왼중지', '왼새끼', '오른중지', '오른엄지', '오른중지', '오른검지', '왼엄지', '왼검지', '오른새끼', '오른검지', '왼엄지', '오른중지', '왼검지', '왼새끼', '오른검지', '왼약지', '오른새끼', '오른엄지', '왼약지', '왼중지', '왼새끼', '오른약지'),
  value = c(val1, val2, val3)
)
df

           group   finger value
1    일반 마우스   왼중지  1.84
2    일반 마우스   왼검지  2.67
3    일반 마우스 오른약지  2.61
4    일반 마우스   왼약지  2.95
5    일반 마우스   왼엄지  2.25
6    일반 마우스 오른약지  2.35
7    일반 마우스 오른새끼  2.85
8    일반 마우스 오른엄지  2.58
9    일반 마우스   왼중지  3.08
10   일반 마우스   왼새끼  2.25
11     트랙 패트 오른중지  1.79
12     트랙 패트 오른엄지  1.98
13     트랙 패트 오른중지  2.01
14     트랙 패트 오른검지  1.93
15     트랙 패트   왼엄지  2.24
16     트랙 패트   왼검지  2.03
17     트랙 패트 오른새끼  2.22
18     트랙 패트 오른검지  1.44
19     트랙 패트   왼엄지  2.24
20     트랙 패트 오른중지  2.05
21 버티컬 마우스   왼검지  3.31
22 버티컬 마우스   왼새끼  2.24
23 버티컬 마우스 오른검지  2.74
24 버티컬 마우스   왼약지  2.36
25 버티컬 마우스 오른새끼  2.79
26 버티컬 마우스 오른엄지  2.20
27 버티컬 마우스   왼약지  2.32
28 버티컬 마우스   왼중지  2.82
29 버티컬 마우스   왼새끼  2.73
30 버티컬 마우스 오른약지  2.78

• 요인: 클릭하는 장치 종류
• 수준: 일반 마우스, 트랙 패드, 버티컬 마우스
• 반응치: 클릭 반응속도

10개의 손가락에 대해 3개의 장치를 랜덤으로 사용하여 클릭 반응속도를 측정한다.

각 손가락의 실험에 대해 랜덤으로 그룹을 나눈 후, 그룹별로 클릭하는 장치 종류를 배정하였다.

b

df.means <- tapply(df$value, INDEX=df$group, FUN=mean)
boxplot(df$value ~ df$group, col=c("lightblue", "mistyrose", "lightcyan"))
points(1:3, df.means, col="red", pch=4, cex=1.5)

결과는 다음과 같이 나온다.

c

df.sd <- tapply(df$value, INDEX=df$group, FUN=sd)
df.sd.diff <- max(df.sd) / min(df.sd)
if (df.sd.diff > 2) 
{
  print("모집단의 분산이 동일하지 않음")
} else 
{
  print("모집단의 분산이 동일하다고 가정")
}

[1] "모집단의 분산이 동일하다고 가정"

결과는 다음과 같이 나온다.

d

library(ggpubr)

Loading required package: ggplot2

ggqqplot(val1)

ggqqplot(val2)

ggqqplot(val3)

그림을 보니 반응치 값들이 정규분포를 따르는 것 같다!

e

df.anova <- aov(value ~ group, data=df)
summary(df.anova)

            Df Sum Sq Mean Sq F value   Pr(>F)    
group        2  2.381  1.1907   11.17 0.000292 ***
Residuals   27  2.878  0.1066                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

is_significant <- summary(df.anova)[[1]][["Pr(>F)"]][1] < 0.05
if (is_significant)
{
  print("95%에서 처리별 모평균의 차이가 있음")
} else
{
  print("95%에서 처리별 모평균의 차이가 없음")
}

[1] "95%에서 처리별 모평균의 차이가 있음"

결과는 다음과 같이 나온다.

f

if (is_significant)
{
  df.bon <- pairwise.t.test(df$value, df$group, p.adjust.method = "bonferroni")
  diff_pair <- which(df.bon$p.value < 0.05, arr.ind = TRUE)
  if (length(diff_pair) > 0)
  {
    cat("모평균의 차이가 있는 쌍", "\n")
    for (i in 1:nrow(diff_pair)) 
    {
      cat(colnames(df.bon$p.value)[diff_pair[i, "col"]], "-", rownames(df.bon$p.value)[diff_pair[i, "row"]], "\n")
    }
  } else 
  {
    print("모평균의 차이가 있는 처리 쌍 없음")
  }
}

모평균의 차이가 있는 쌍 
버티컬 마우스 - 트랙 패트 
일반 마우스 - 트랙 패트 

결과는 다음과 같이 나온다.

ANOVA for Randomized Block Design

a

df <- data.frame(
  block = rep(c("아스팔트", "트랙", "모래밭", "잔디밭"), each=3),
  treatment = rep(c("런닝화", "축구화", "크록스"), times=4),
  value = c(6.1, 6.4, 6.5, 5.5, 5.9, 6.0, 6.9, 7.1, 7.5, 6.3, 6.9, 7.0)
)
df

      block treatment value
1  아스팔트    런닝화   6.1
2  아스팔트    축구화   6.4
3  아스팔트    크록스   6.5
4      트랙    런닝화   5.5
5      트랙    축구화   5.9
6      트랙    크록스   6.0
7    모래밭    런닝화   6.9
8    모래밭    축구화   7.1
9    모래밭    크록스   7.5
10   잔디밭    런닝화   6.3
11   잔디밭    축구화   6.9
12   잔디밭    크록스   7.0

• 요인: 운동화 종류
• 수준: 런닝화, 축구화, 크록스
• block: 달리는 땅
• 반응치: 50m 달리기 시간(초)

각 block에 대해 3개의 운동화 종류를 사용하는 순서를 랜덤으로 결정해서 달리기 시간을 측정한다.

b

df.anova.rbd <- aov(value ~ treatment + block, data=df)
summary(df.anova.rbd)

            Df Sum Sq Mean Sq F value   Pr(>F)    
treatment    2 0.6317  0.3158   27.73  0.00093 ***
block        3 3.0492  1.0164   89.24 2.28e-05 ***
Residuals    6 0.0683  0.0114                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

처리에 의한 변동이 통계적으로 유의미하다.

block에 의한 변동 역시 통계적으로 유의미하다.

c

df.anova <- aov(value~treatment, data=df)
summary(df.anova)

            Df Sum Sq Mean Sq F value Pr(>F)
treatment    2 0.6317  0.3158   0.912  0.436
Residuals    9 3.1175  0.3464               

처리에 의한 변동이 통계적으로 유의미하지 않다고 나온다.

block에 의한 변동이 통계적으로 유의미하기 때문에, block에 의한 변동을 제거하고 처리에 의한 변동을 분석해야 하기 때문이다.

Simple Linear Regression

a

x <- runif(100, 0, 10)
error <- rnorm(100, 0, 4)
y <- 3 * x - 2 + error
model <- lm(y ~ x)
model

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)            x  
     -2.248        2.933  

결과는 다음과 같이 나온다.

b

cat("B1의 추정 기울기: ", coef(model)[2])

B1의 추정 기울기:  2.933282

trust <- confint(model, level=0.95)[2, ]
cat("신뢰구간: ", trust, "\n")

신뢰구간:  2.652931 3.213632 

if (3 > trust[1] && 3 < trust[2]) 
{
  print("신뢰구간에 3 포함")
} else 
{
  print("신뢰구간에 3 안 포함")
}

[1] "신뢰구간에 3 포함"

결과는 다음과 같이 나온다.

c

plot(x, y, cex=0.7)
abline(model, col = "red", lwd = 2)
abline(-2, 3, col = "blue", lwd = 2)
legend("topleft", legend = c("실제 회귀선", "추정 회귀선"), col = c("blue", "red"), lwd = 2)

결과는 다음과 같이 나온다.

d

cnt <- 0
for (i in 1:100) 
{
  x <- runif(100, 0, 10)
  error <- rnorm(100, 0, 4)
  y <- 3 * x - 2 + error
  model <- lm(y ~ x)
  trust <- confint(model, level=0.95)[2, ]
  cnt <- cnt + (3 > trust[1] && 3 < trust[2])
}
cnt

[1] 98

95에 가깝게 나온다.

Multiple Linear Regression

a

data(iris)
model <- lm(Sepal.Width ~ Sepal.Length + Petal.Length + Petal.Width, data = iris)
summary(model)

Call:
lm(formula = Sepal.Width ~ Sepal.Length + Petal.Length + Petal.Width, 
    data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.88045 -0.20945  0.01426  0.17942  0.78125 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   1.04309    0.27058   3.855 0.000173 ***
Sepal.Length  0.60707    0.06217   9.765  < 2e-16 ***
Petal.Length -0.58603    0.06214  -9.431  < 2e-16 ***
Petal.Width   0.55803    0.12256   4.553  1.1e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3038 on 146 degrees of freedom
Multiple R-squared:  0.524, Adjusted R-squared:  0.5142 
F-statistic: 53.58 on 3 and 146 DF,  p-value: < 2.2e-16

F 값의 p-value가 매우 작으므로, 모델이 통계적으로 유의미하다고 할 수 있다.

각각의 독립변수에 대한 p-value 역시 모두 매우 작으므로, 종속변수에 통계적으로 유의미한 영향을 미친다고 할 수 있다.

하지만 r-squared 값이 크지 않아서 모델이 종속변수의 변동을 잘 설명하지 못한다고 할 수 있다.

b

plot(model, 1)

잔차가 U자 패턴을 보이므로, 선형성이 만족되지 않는 것 같다.

c

model2 <- lm(Sepal.Width ~ Sepal.Length + I(Sepal.Length^2) + Petal.Length + I(Petal.Length^2) + Petal.Width + I(Petal.Width^2), data = iris)
summary(model2)

Call:
lm(formula = Sepal.Width ~ Sepal.Length + I(Sepal.Length^2) + 
    Petal.Length + I(Petal.Length^2) + Petal.Width + I(Petal.Width^2), 
    data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.82277 -0.16843 -0.00315  0.15300  0.77761 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -3.10783    1.37460  -2.261 0.025275 *  
Sepal.Length       2.32243    0.50141   4.632 8.08e-06 ***
I(Sepal.Length^2) -0.15699    0.04264  -3.682 0.000327 ***
Petal.Length      -0.89155    0.20300  -4.392 2.17e-05 ***
I(Petal.Length^2)  0.06925    0.02336   2.965 0.003549 ** 
Petal.Width       -0.03666    0.38214  -0.096 0.923708    
I(Petal.Width^2)   0.13095    0.10529   1.244 0.215648    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2755 on 143 degrees of freedom
Multiple R-squared:  0.6167,    Adjusted R-squared:  0.6006 
F-statistic: 38.35 on 6 and 143 DF,  p-value: < 2.2e-16

d

Sepal.Length, \(\text{Sepal.Length}^2\), Petal.Length의 p-value가 모두 0.05보다 작으므로, 이 변수들이 종속변수에 통계적으로 유의미한 영향을 미친다고 할 수 있다.

r-squared 값도 더 작아져서, c 모델이 b 모델보다 종속변수의 변동을 잘 설명한다고 할 수 있다.

e

plot(model2, 1)

U자 패턴이 완만해진걸로 보인다.