import numpy as np
import matplotlib.pyplot as plt
X = 2 * np.random.rand(100, 1)
y = 6 + 4 * X + np.random.randn(100, 1)
plt.scatter(X, y)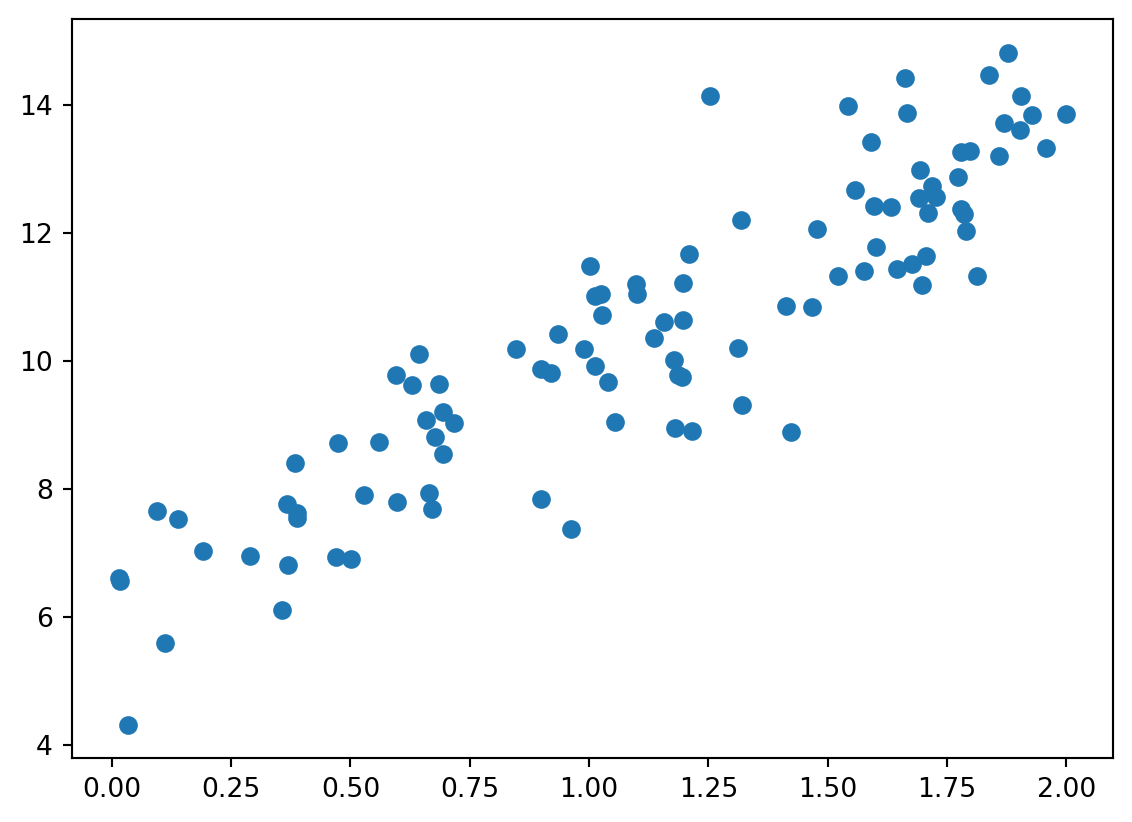
2025년 7월 28일

import numpy as np
import matplotlib.pyplot as plt
X = 2 * np.random.rand(100, 1)
y = 6 + 4 * X + np.random.randn(100, 1)
plt.scatter(X, y)
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred)) / N
return cost
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
y_pred = np.dot(X, w1.T) + w0
diff = y - y_pred
w1_update = -(2/N) * learning_rate * np.dot(X.T, diff)
w0_update = -(2/N) * learning_rate * np.sum(diff)
return w1_update, w0_update
def gradient_descent_steps(X, y, iters=10000):
w0 = np.zeros((1, 1))
w1 = np.zeros((1, 1))
for _ in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0w1, w0 = gradient_descent_steps(X, y, iters=1000)
y_pred = w1[0, 0] * X + w0
print(f'w0: {w0[0, 0]:.3f} w1: {w1[0, 0]:.3f}, total cost: {get_cost(y, y_pred):.3f}')
plt.scatter(X, y)
plt.plot(X, y_pred)w0: 5.955 w1: 3.940, total cost: 1.018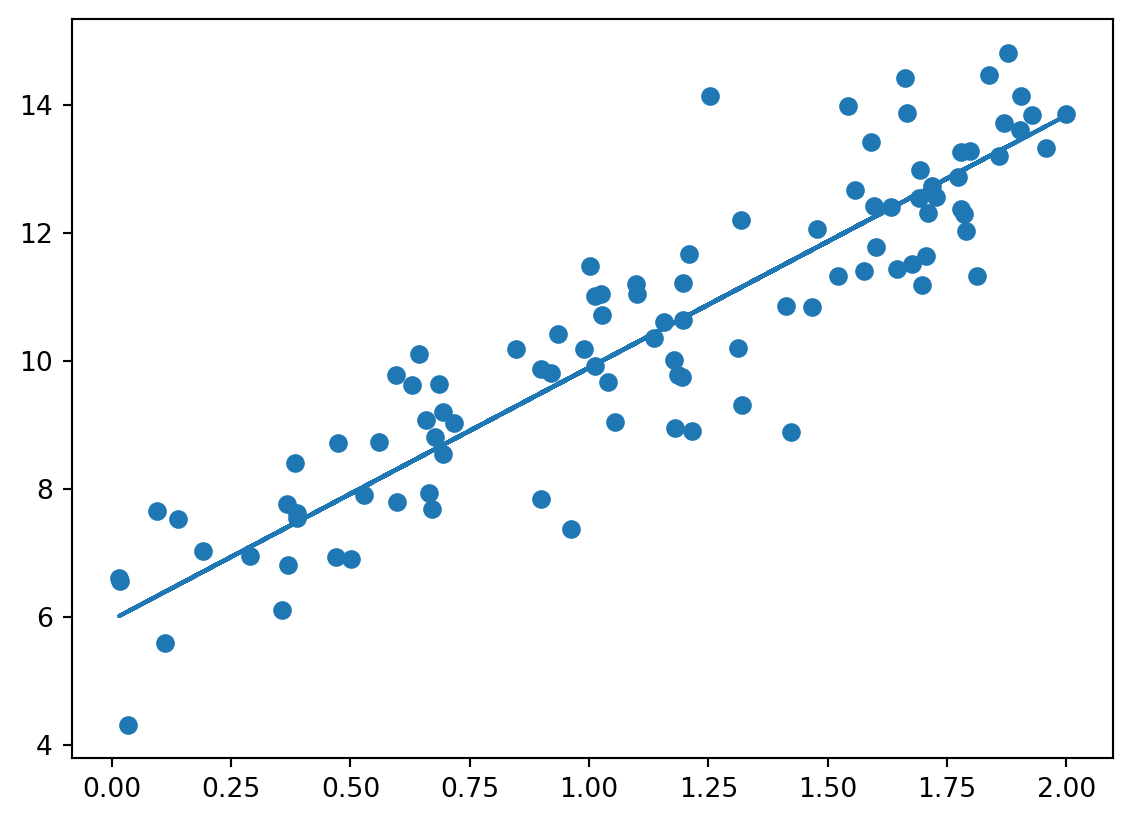
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1, 1))
w1 = np.zeros((1, 1))
for ind in range(iters):
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0boston 데이터가 윤리적 문제로 사용 불가능하다고 한다.
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
y_target = df['price']
X_data = df.drop(['price'], axis=1, inplace=False)
lr = LinearRegression()
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring="neg_mean_squared_error", cv=5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)cross_val_score는 값이 큰걸 좋게 평가해서 neg를 기준으로 넣어줘야함
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
def polynominal_func(X):
y = 1 + 2 * X[:, 0] + 3 * X[:, 0]**2 + 4 * X[:, 1]**3
return y
model = Pipeline([('poly', PolynomialFeatures(degree=3)),
('linear', LinearRegression())])
X = np.arange(4).reshape(2, 2)
y = polynominal_func(X)
model = model.fit(X, y)
np.round(model.named_steps['linear'].coef_, 2)array([0. , 0.18, 0.18, 0.36, 0.54, 0.72, 0.72, 1.08, 1.62, 2.34])L2 규제(Ridge): \(min(RSS(W) + \lambda ||W||^2)\)
L1 규제(Lasso): \(min(RSS(W) + \lambda ||W||_1)\)
λ가 크면, 회귀계수의 크기가 작아지고, λ가 0이 되면 일반 선형회귀와 같아짐
L1 규제는 영향력이 작은 피처의 계수를 0으로 만들어서 피처 선택 효과가 있음. L2는 0으로 만들지는 않음
import pandas as pd
from sklearn.linear_model import Ridge, Lasso, ElasticNet
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None):
coeff_df = pd.DataFrame()
for param in params:
if model_name == 'Ridge':
model = Ridge(alpha=param)
elif model_name == 'Lasso':
model = Lasso(alpha=param)
elif model_name == 'ElasticNet':
model = ElasticNet(alpha=param, l1_ratio=0.7)
neg_mse_scores = cross_val_score(model, X_data_n, y_target_n, scoring="neg_mean_squared_error", cv=5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(f'{param}: {avg_rmse:.3f}')
model.fit(X_data_n, y_target_n)
coeff = pd.Series(data=model.coef_, index=X_data_n.columns)
colname = 'alpha:' + str(param)
coeff_df[colname] = coeff
return coeff_df