import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Noto Sans KR'
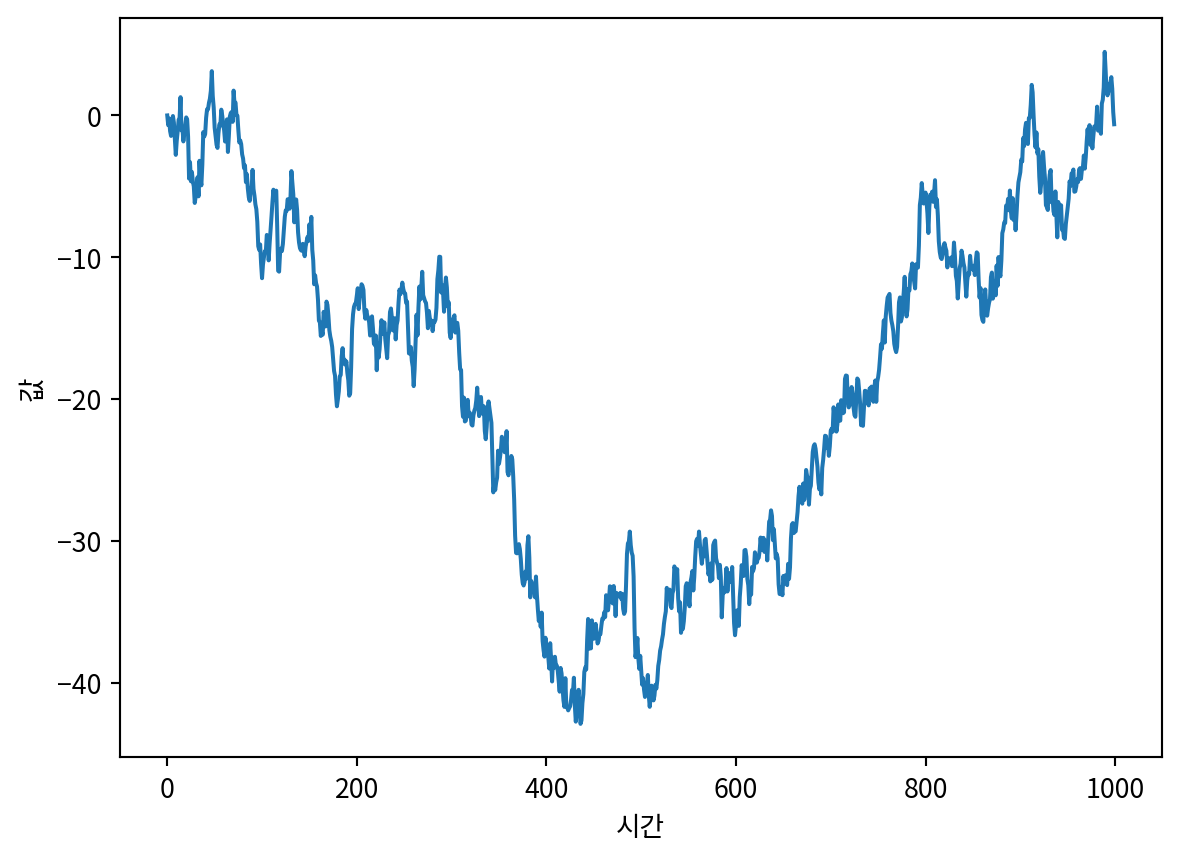
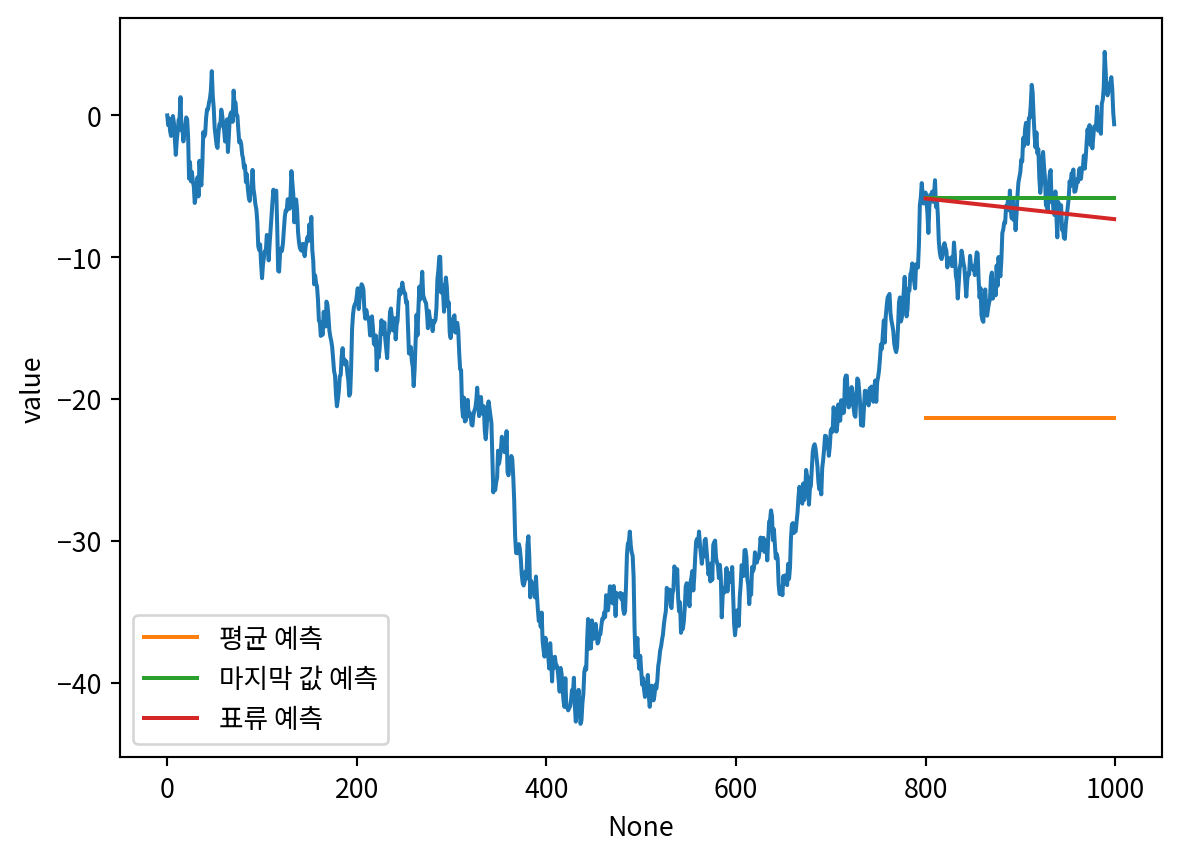
steps = np.random.standard_normal(1000)
steps[0] = 0
random_walk = np.cumsum(steps)
sns.lineplot(x=np.arange(len(random_walk)), y=random_walk)
plt.xlabel('시간')
plt.ylabel('값')Text(0, 0.5, '값')