def odds(p):
return p / (1 - p)
def prob(o):
return o / (1 + o)
def prob2(a, b):
return a / (a + b)
odds(0.6)1.49999999999999982025년 6월 20일

\(odds(A|D) = odds(A) \cdot \frac{P(D|A)}{P(D|B)}\)
1.5\(odds(A|D) = odds(A) \cdot \frac{P(D|A)}{P(D|B)}\) \(→ \frac{odds(A|D)}{odds(A)} = \frac{P(D|A)}{P(D|B)}\)
like1 = 0.01 # oliver가 혈흔을 남긴 경우
like2 = 2 * 0.6 * 0.01 # oliver가 혈흔을 남기지 않은 경우
likelihood_ratio = like1 / like2
likelihood_ratio0.8333333333333334from scipy.stats import binom
from empiricaldist import Pmf
import numpy as np
import matplotlib.pyplot as plt
def make_binomial(n, p):
ks = np.arange(n+1)
ps = binom.pmf(ks, n, p)
return Pmf(ps, ks)
dist_sensitive = make_binomial(num_sensitive, 0.95)
dist_insensitive = make_binomial(num_insensitive, 0.40)
dist_total = Pmf.add_dist(dist_sensitive, dist_insensitive)
dist_sensitive.plot(label='sensitive', ls=':')
dist_insensitive.plot(label='insensitive', ls='--')
dist_total.plot(label='total')
plt.legend()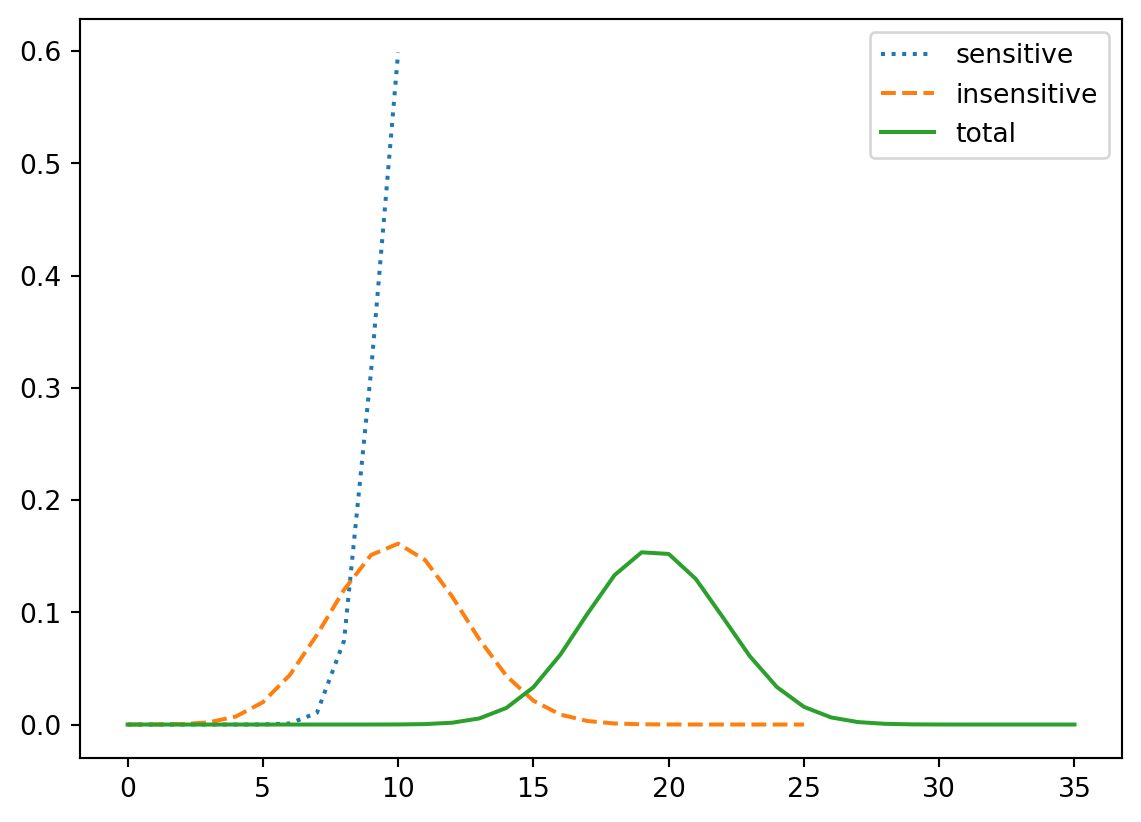
import pandas as pd
table = pd.DataFrame()
for num_sensitive in range(0, n+1):
num_insensitive = n - num_sensitive
dist_sensitive = make_binomial(num_sensitive, 0.95)
dist_insensitive = make_binomial(num_insensitive, 0.40)
dist_total = Pmf.add_dist(dist_sensitive, dist_insensitive)
table[num_sensitive] = dist_total
for dist in table:
table[dist].plot(label=f'num_sensitive = {dist}')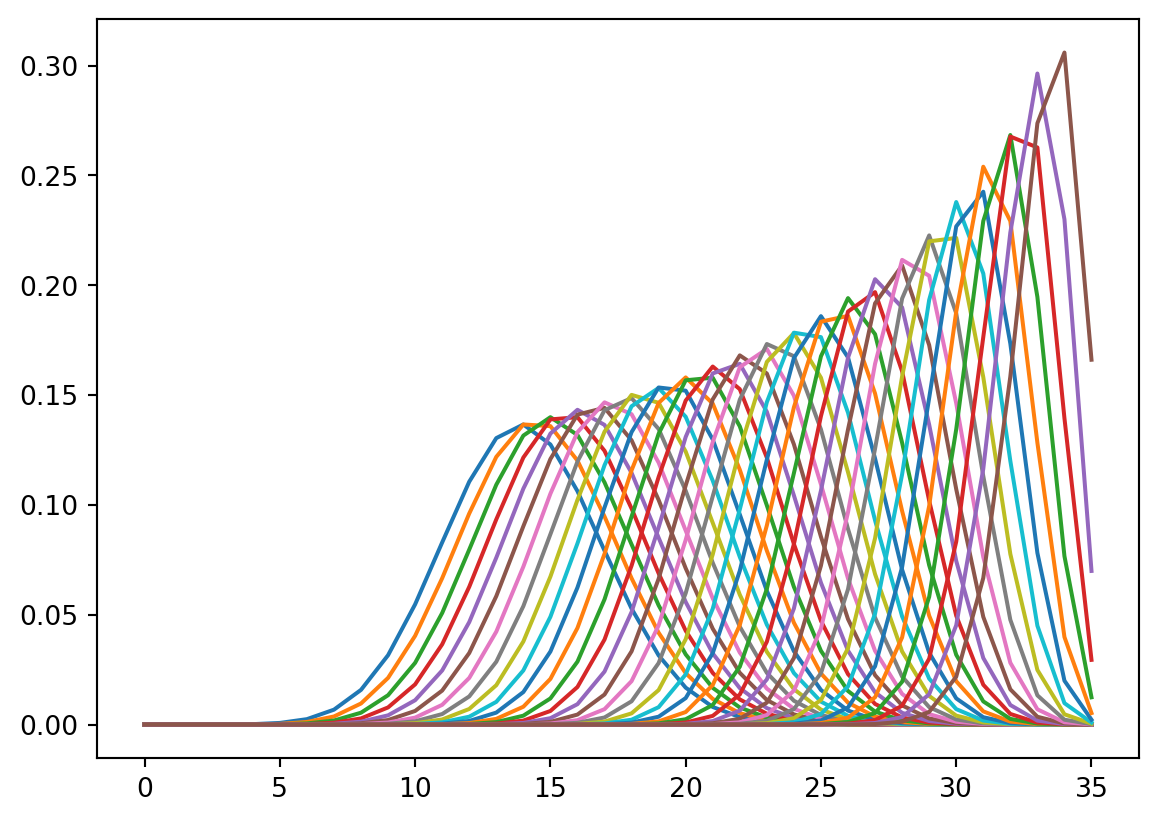
likelihood1 = table.loc[12]
hypos = np.arange(n+1)
prior = Pmf(1, hypos)
posterior1 = prior * likelihood1
posterior1.normalize()
likelihood2 = table.loc[20]
posterior2 = prior * likelihood2
posterior2.normalize()
plt.rcParams['font.family'] = 'Noto Sans KR'
posterior1.plot(label='12개가 정확히 분류한 경우의 사후분포', color='C4')
posterior2.plot(label='20개가 정확히 분류한 경우의 사후분포', color='C5')
plt.legend()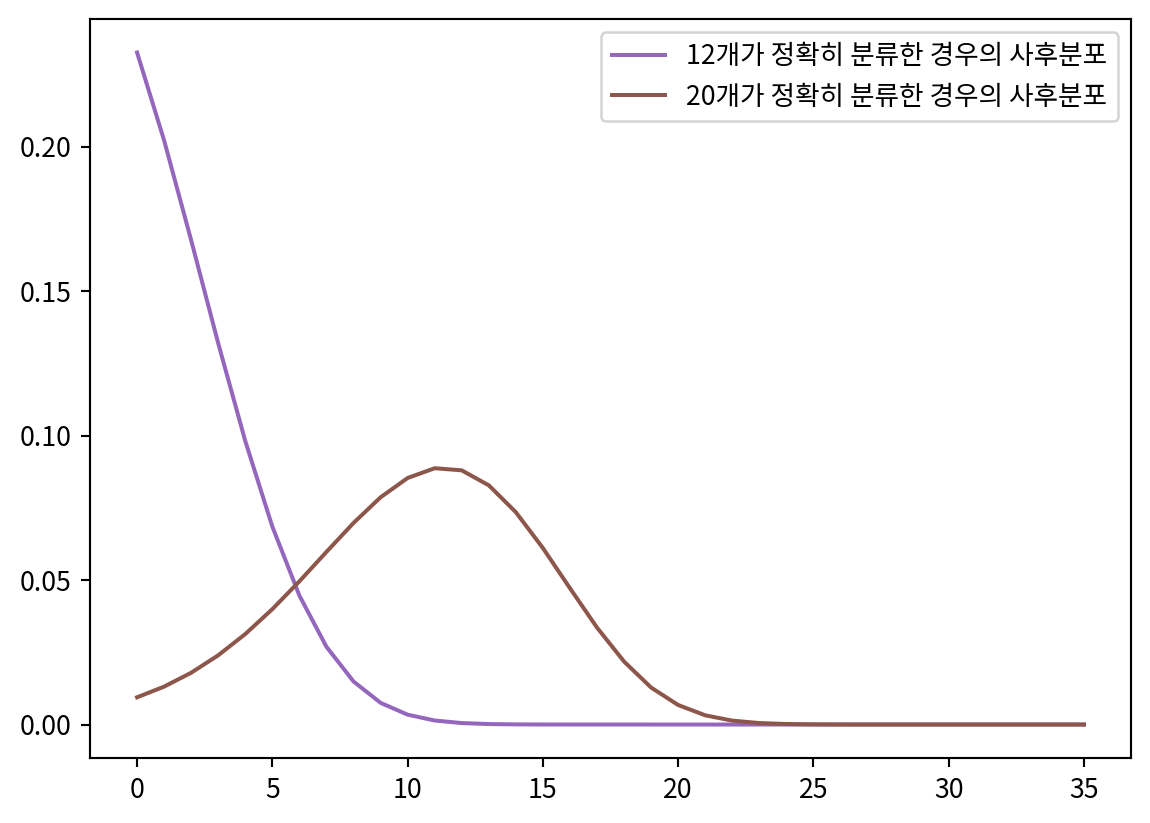
dice6 = Pmf.from_seq(np.arange(1, 7))
goblin_health = dice6.add_dist(dice6)
remaining_health = Pmf.sub_dist(goblin_health, 3)
attack_damage = dice6
defeat_probability = 0
for damage, damage_prob in attack_damage.items():
for remaining, remaining_prob in remaining_health.items():
if remaining > 0 and damage > remaining:
defeat_probability += damage_prob * remaining_prob
print(f"\n고블린을 물리칠 확률: {defeat_probability:.3f}")
고블린을 물리칠 확률: 0.292pmf = Pmf(1, ['long', 'zost', 'bell'])
pmf.normalize()
dice = Pmf([1/3] * 3, np.arange(0, 3))
like = [dice.add_dist(dice).add_dist(dice).add_dist(dice).add_dist(dice),
dice.add_dist(dice).add_dist(dice).add_dist(dice),
dice.add_dist(dice).add_dist(dice)]
df = pd.DataFrame(like).fillna(0).transpose()
for i in [3, 4, 5]:
pmf *= np.array(df.loc[i])
pmf.normalize()
pmf| probs | |
|---|---|
| long | 0.235762 |
| zost | 0.449704 |
| bell | 0.314534 |
import numpy as np
import pandas as pd
from scipy.stats import binom
from empiricaldist import Pmf
n_total = 538
n_outperform = 312
hypos = np.arange(n_total + 1)
prior = Pmf(1, hypos)
prior.normalize()
likelihoods = np.zeros(prior.shape[0])
for n_honest in hypos:
n_dishonest = n_total - n_honest
honest_dist = make_binomial(n_honest, 0.5)
dishonest_dist = make_binomial(n_dishonest, 0.9)
total_dist = Pmf.add_dist(honest_dist, dishonest_dist)
likelihood = total_dist[n_outperform]
likelihoods[n_honest] = likelihood
posterior = prior * likelihoods
posterior.normalize()
most_likely_honest = posterior.max_prob()
posterior_prob = posterior[most_likely_honest]
print(f"가장 가능성이 높은 정직한 의원 수: {most_likely_honest}명")
print(f"해당 확률: {posterior_prob:.4f}")
# 사후분포 시각화
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 6))
posterior.plot()
plt.xlabel('정직한 의원 수')
plt.ylabel('확률')
plt.title('정직한 의원 수에 대한 사후분포')
plt.axvline(most_likely_honest, color='red', linestyle='--',
label=f'최빈값: {most_likely_honest}명')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
# 95% 신용구간
credible_interval = posterior.credible_interval(0.95)
print(f"95% 신용구간: {credible_interval[0]}명 - {credible_interval[1]}명")가장 가능성이 높은 정직한 의원 수: 430명
해당 확률: 0.0147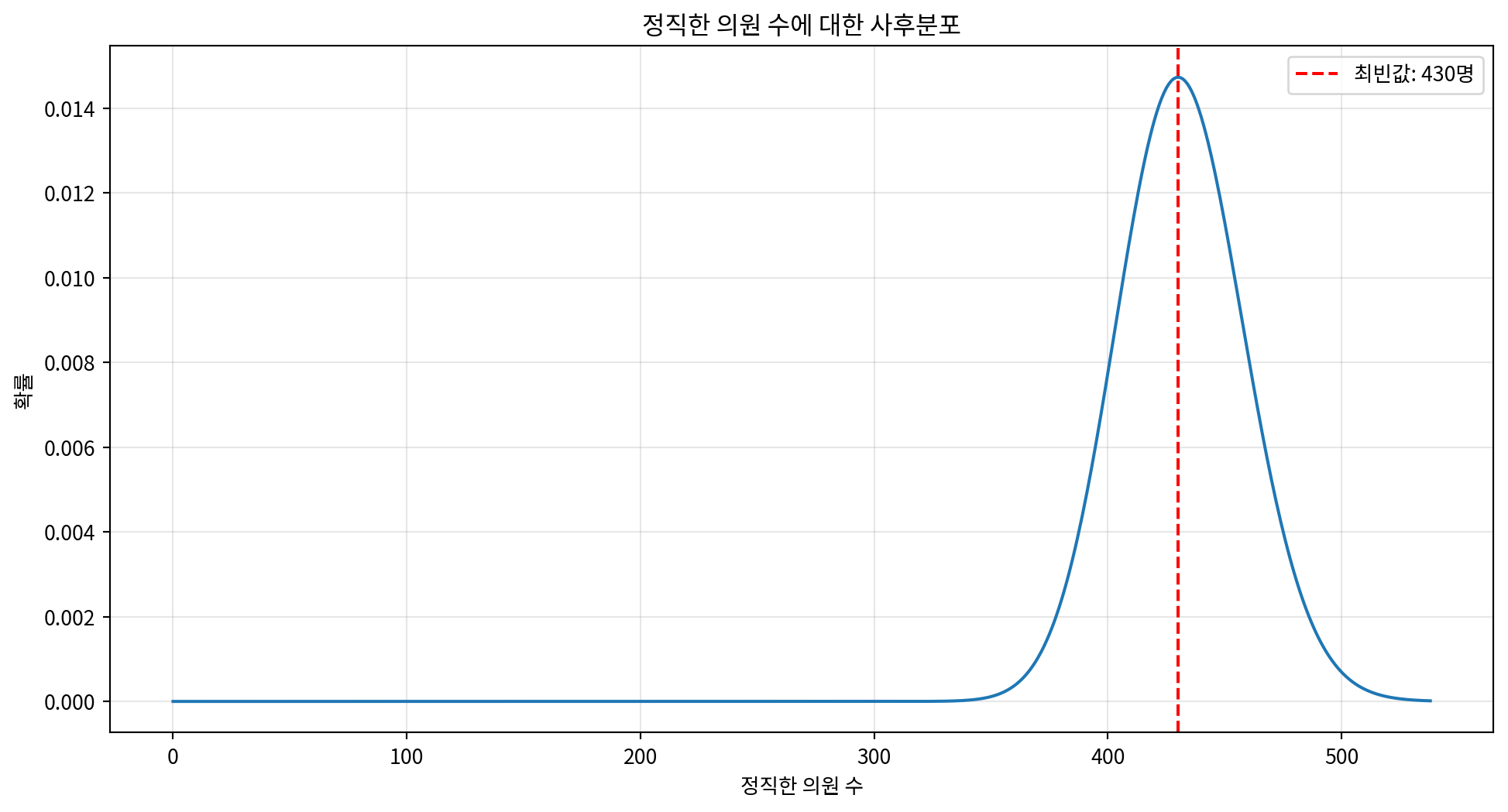
95% 신용구간: 380.0명 - 486.0명