from scipy.stats import binom
from empiricaldist import Pmf
import numpy as np
def make_binominal(n, p):
ks = np.arange(n + 1)
ps = binom.pmf(ks, n, p)
return Pmf(ps, ks)비율 추정
확률 통계

유로 동전 문제
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Noto Sans KR'
pmf_k = make_binominal(n=250, p=0.5)
pmf_k.plot(label='coin', color='C5')
plt.title('coin toss 이항분포')
plt.xlabel('앞면이 나온 횟수(k)')
plt.ylabel('PMF')Text(0, 0.5, 'PMF')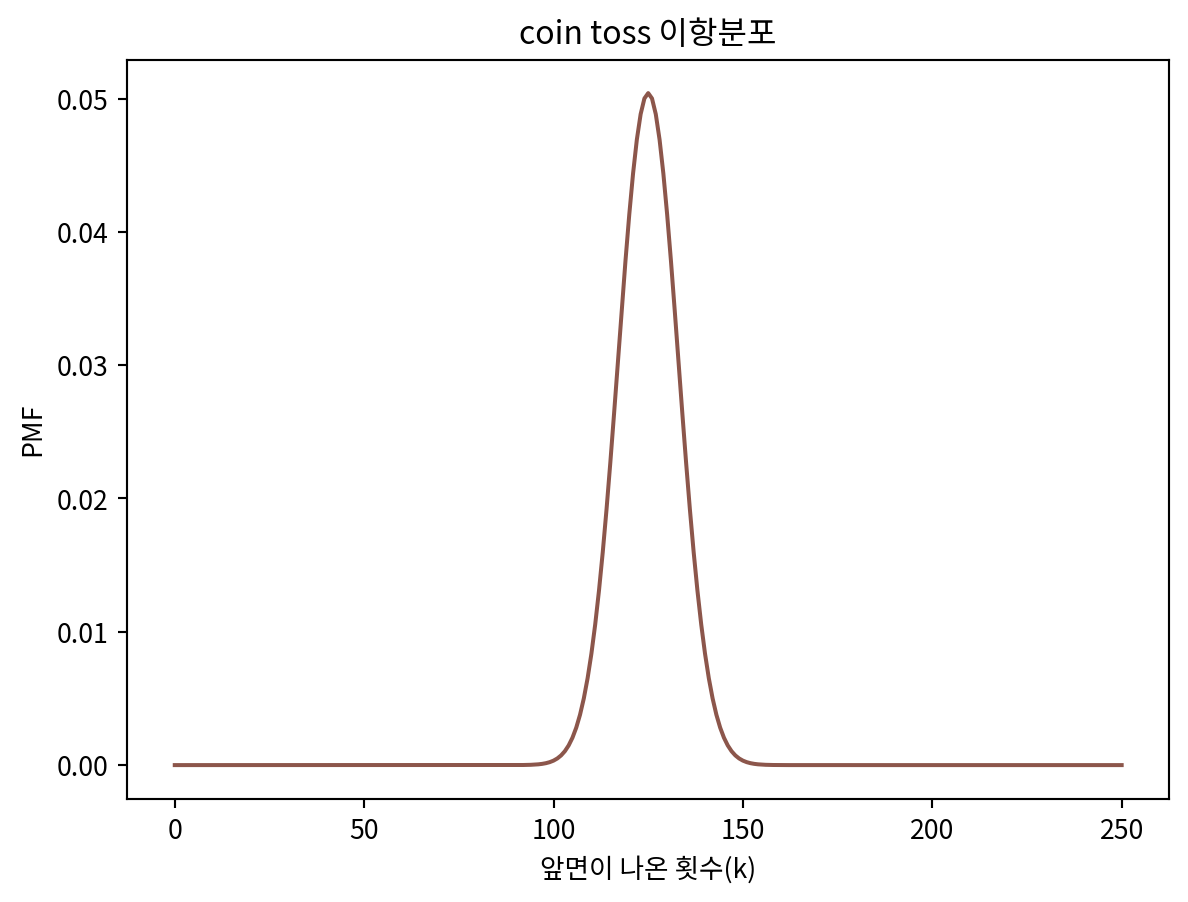
- 동전을 250번 던져서 앞면의 횟수가 140과 같은 극단적인 값이 나올 확률
pmf_k.prob_ge(140) + pmf_k.prob_le(110)0.06642115124004333베이지안 추정
- 동전 앞면의 비율을 균등분포로 가정하고 시작
hypos = np.linspace(0, 1, 101)
prior = Pmf(1, hypos)
likelihood_heads = hypos
likelihood_tails = 1 - hypos
likelihood = {
'H': likelihood_heads,
'T': likelihood_tails
}
prior| probs | |
|---|---|
| 0.00 | 1 |
| 0.01 | 1 |
| 0.02 | 1 |
| 0.03 | 1 |
| 0.04 | 1 |
| ... | ... |
| 0.96 | 1 |
| 0.97 | 1 |
| 0.98 | 1 |
| 0.99 | 1 |
| 1.00 | 1 |
101 rows × 1 columns
def update_euro(pmf, dataset):
for data in dataset:
pmf *= likelihood[data]
pmf.normalize()posterior = prior.copy()
dataset = 'H' * 140 + 'T' * 110
update_euro(posterior, dataset)
posterior.plot(label='coin', color='C5')
plt.title('동전 앞면 비율의 사후확률 분포')
plt.xlabel('동전 앞면의 비율')
plt.ylabel('PMF')Text(0, 0.5, 'PMF')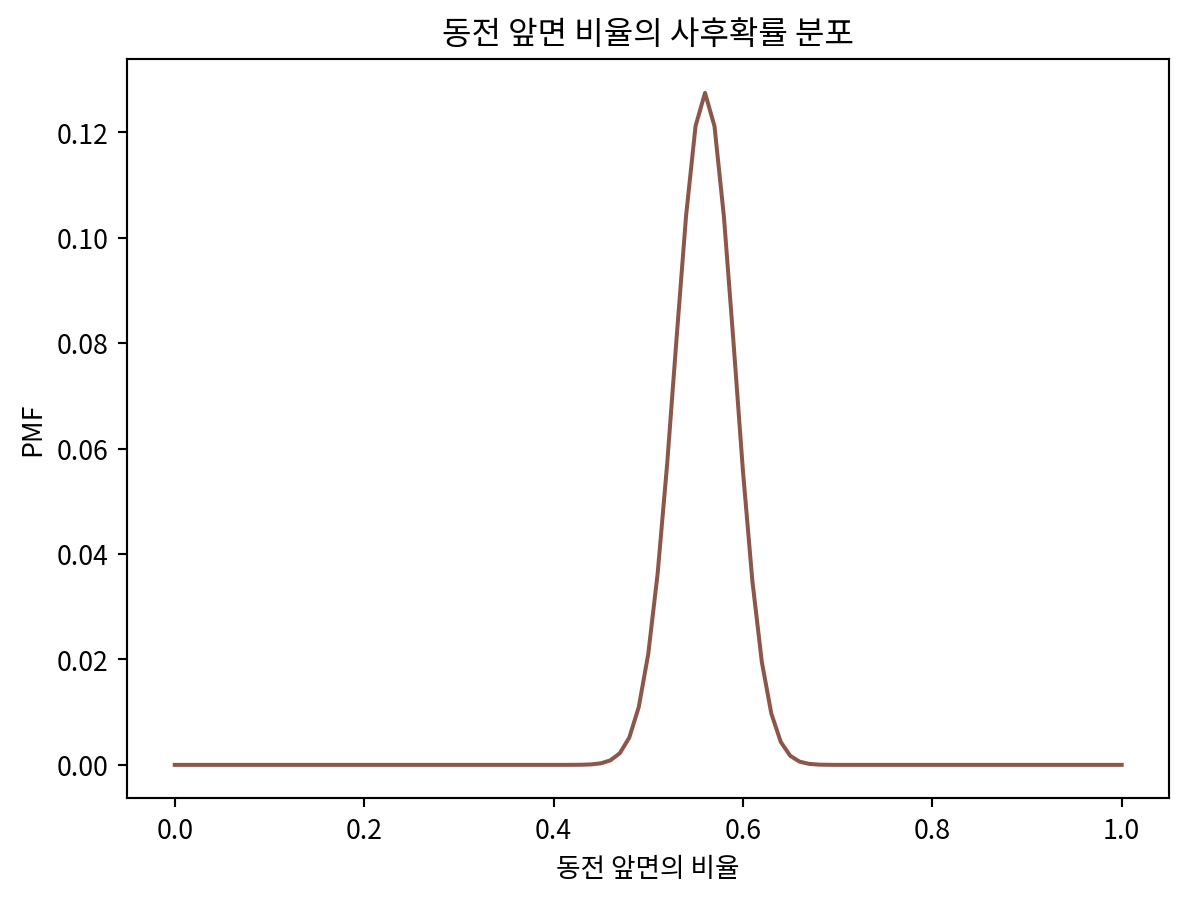
print(f'동전의 앞면이 250번 중 140번 등장했다면 앞면의 비율은 {posterior.max_prob()}일 확률이 가장 높다.')동전의 앞면이 250번 중 140번 등장했다면 앞면의 비율은 0.56일 확률이 가장 높다.삼각사전분포
- 사전확률을 균등분포로 설정했지만, 실제로는 정규분포에 가까울 것이다.
- 근데 책에서는 일단 삼각분포를 사용한다.
ramp_up = np.arange(50)
ramp_down = np.arange(50, -1, -1)
a = np.append(ramp_up, ramp_down)
triangle = Pmf(a, hypos, name='triangle')
triangle.normalize()
uniform = Pmf(1, hypos, name='uniform')
uniform.normalize()
uniform.plot(label='균등사전', color='C4')
triangle.plot(label='삼각사전', color='C5')
plt.legend()
plt.title('삼각사전분포 및 균등사전분포')
plt.xlabel('동전 앞면의 비율')
plt.ylabel('PMF')Text(0, 0.5, 'PMF')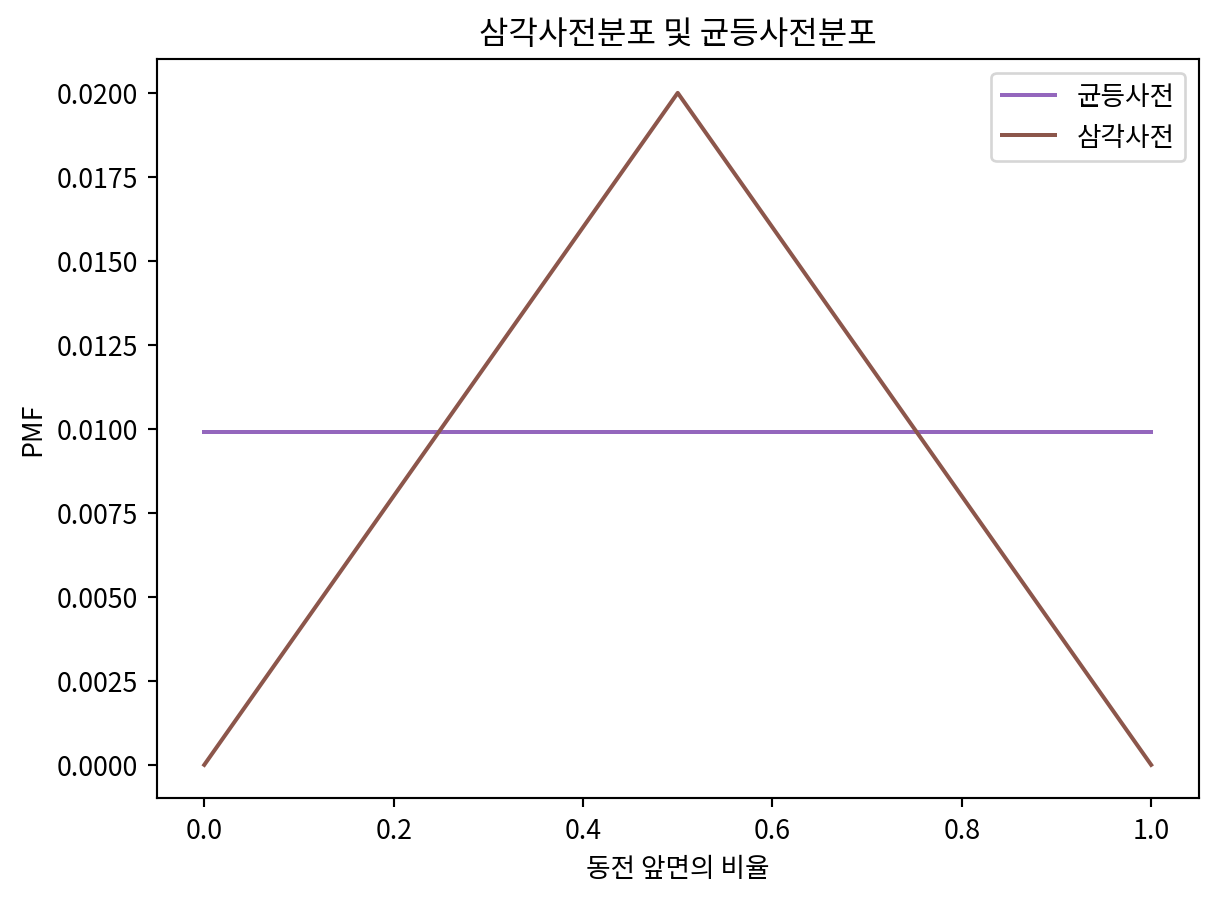
update_euro(uniform, dataset)
update_euro(triangle, dataset)
uniform.plot(label='균등사전', color='C4')
triangle.plot(label='삼각사전', color='C5')
plt.legend()
plt.title('삼각 및 균등 사후분포')
plt.xlabel('동전 앞면의 비율')
plt.ylabel('PMF')Text(0, 0.5, 'PMF')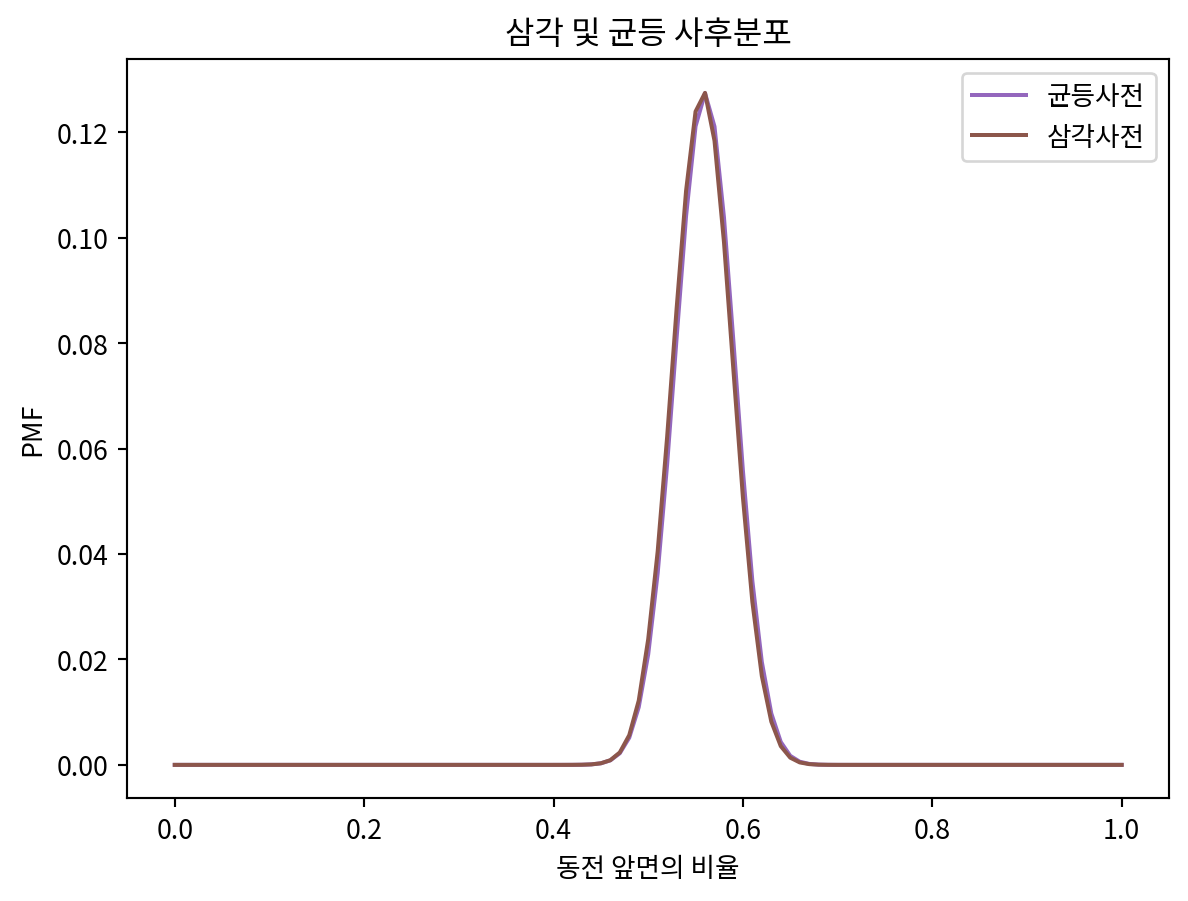
- 두 확률분포의 사후 분포간 차이는 미미함.
- 데이터가 충분하다면 서로 다른 사전확률로 시작한다고 해도 동일한 사후확률로 수렴하는 경향이 있다.
이항가능도함수
- 갱신을 굳이 250번 하지 않아도, 이항분포를 통해 가능도를 한번에 계산할 수 있다.
def update_binomial(pmf, data):
k, n = data
xs = pmf.qs
likelihood = binom.pmf(k, n, xs)
pmf *= likelihood
pmf.normalize()uniform2 = Pmf(1, hypos, name='uniform2')
data = 140, 250
update_binomial(uniform2, data)
np.allclose(uniform, uniform2)True연습문제
4-1
hypos = np.linspace(0.2, 0.33, 101)
uniform = Pmf(1, hypos)
prior = uniform.copy()
prior.normalize()
data = 3, 3
update_binomial(uniform, data)
prior.plot(label='사전', color='C4')
uniform.plot(label='사후', color='C5')
plt.legend()
plt.title('사전 vs 사후 분포')
plt.xlabel('안타 비율')
plt.ylabel('PMF')Text(0, 0.5, 'PMF')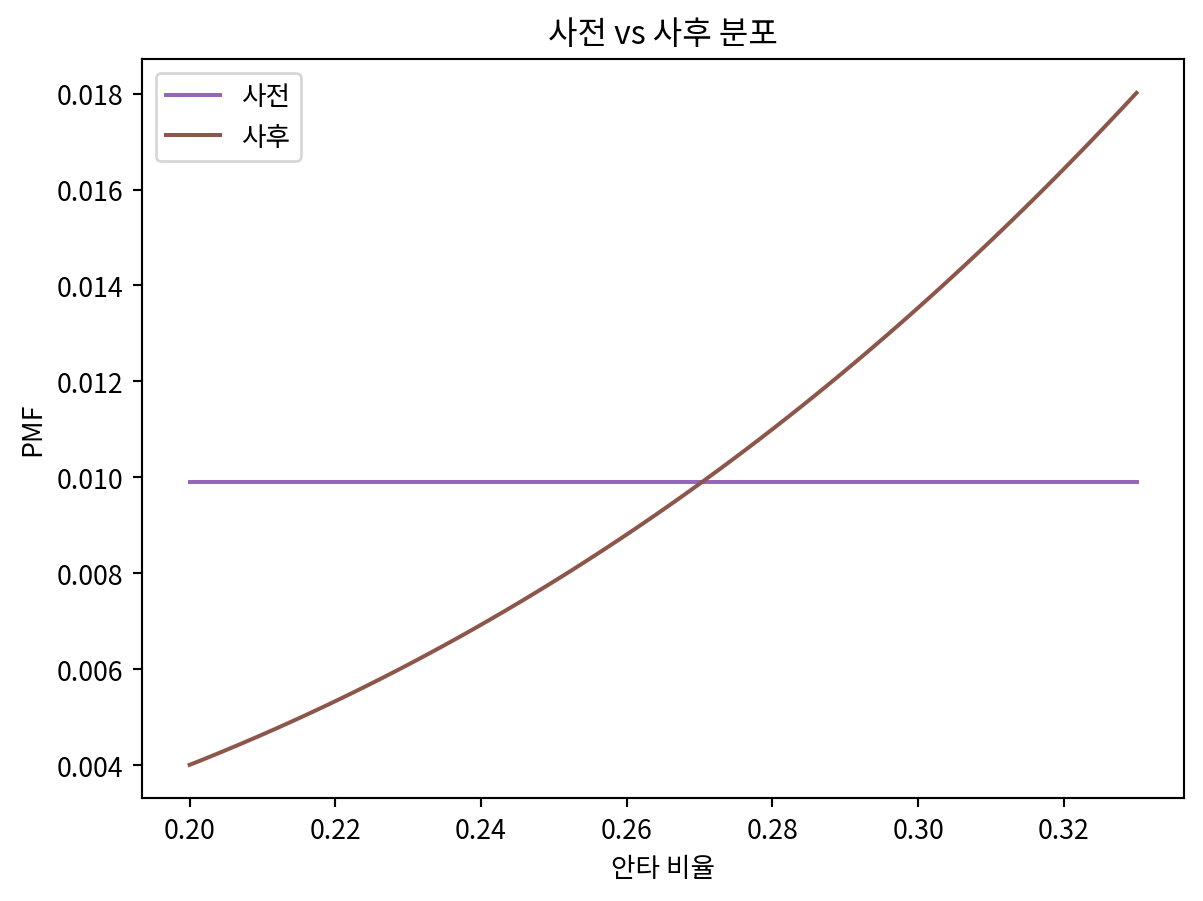
4-2
def update_randomized_response(pmf, data):
yes_count, total = data
ps = pmf.qs
prob_yes = 0.5 + 0.5 * ps
likelihood = binom.pmf(yes_count, total, prob_yes)
pmf *= likelihood
pmf.normalize()
hypos = np.linspace(0, 1, 101)
uniform = Pmf(1, hypos)
prior = uniform.copy()
prior.normalize()
data = 80, 100
update_randomized_response(uniform, data)
prior.plot(label='사전', color='C4')
uniform.plot(label='사후', color='C5')
plt.legend()
plt.title('Randomized Response - 사전 vs 사후 분포')
plt.xlabel('탈세자 비율 (p)')
plt.ylabel('PMF')
plt.grid(True, alpha=0.3)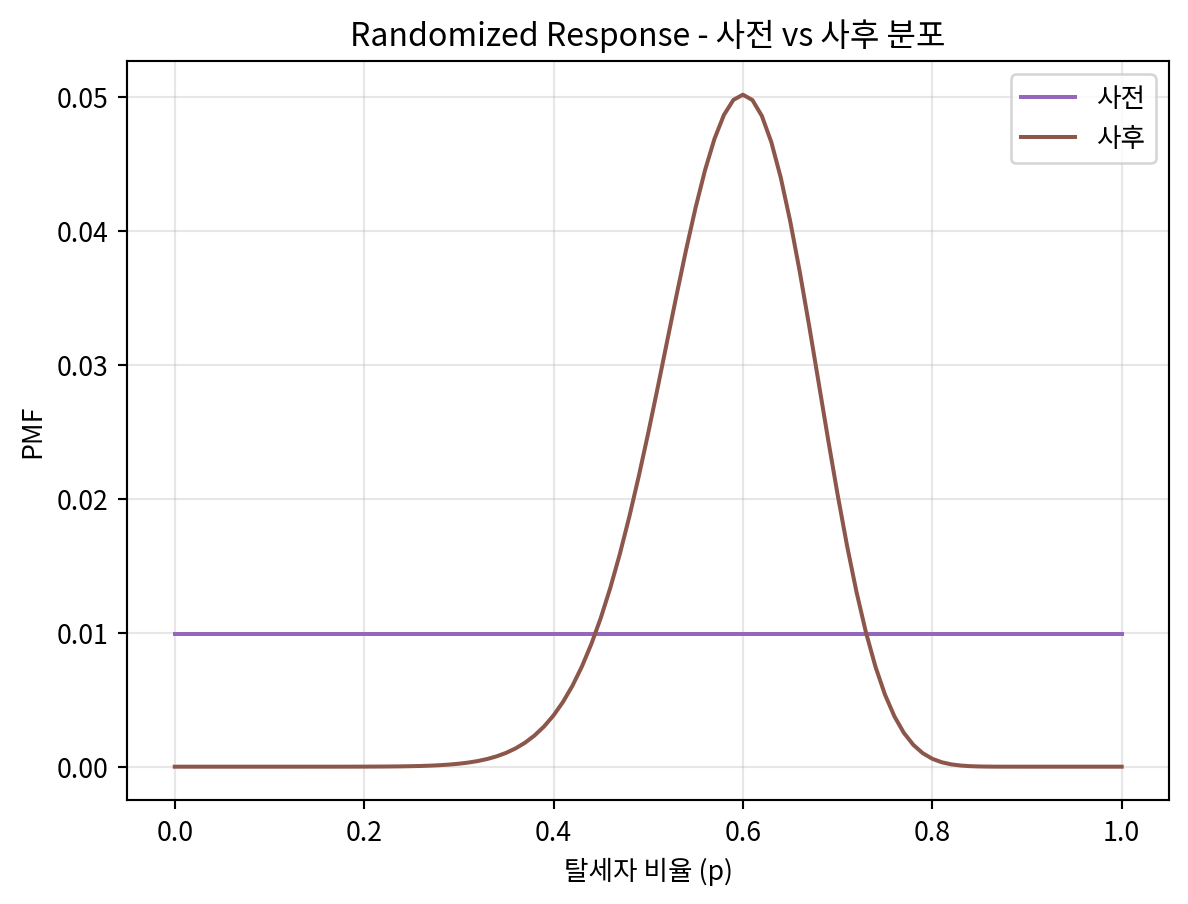
most_likely_rate = uniform.max_prob()
print(f'가장 가능성이 높은 탈세자 비율: {most_likely_rate:.3f}')
credible_interval = uniform.credible_interval(0.95)
print(f'95% 신뢰구간: [{credible_interval[0]:.3f}, {credible_interval[1]:.3f}]')가장 가능성이 높은 탈세자 비율: 0.600
95% 신뢰구간: [0.420, 0.730]4-3
def update_machine_response(pmf, data, y):
k, n = data
xs = pmf.qs * (1 - y) + (1 - pmf.qs) * y
likelihood = binom.pmf(k, n, xs)
pmf *= likelihood
pmf.normalize()
hypos = np.linspace(0, 1, 101)
uniform = Pmf(1, hypos)
data = 140, 250
for y in np.linspace(0, 0.5, 6):
dist = uniform.copy()
update_machine_response(dist, data, y)
dist.plot(label=f'y={y:.1f}')
plt.legend()
plt.title('y에 따른 앞면의 비율')
plt.xlabel('동전 앞면의 비율')
plt.ylabel('PMF')Text(0, 0.5, 'PMF')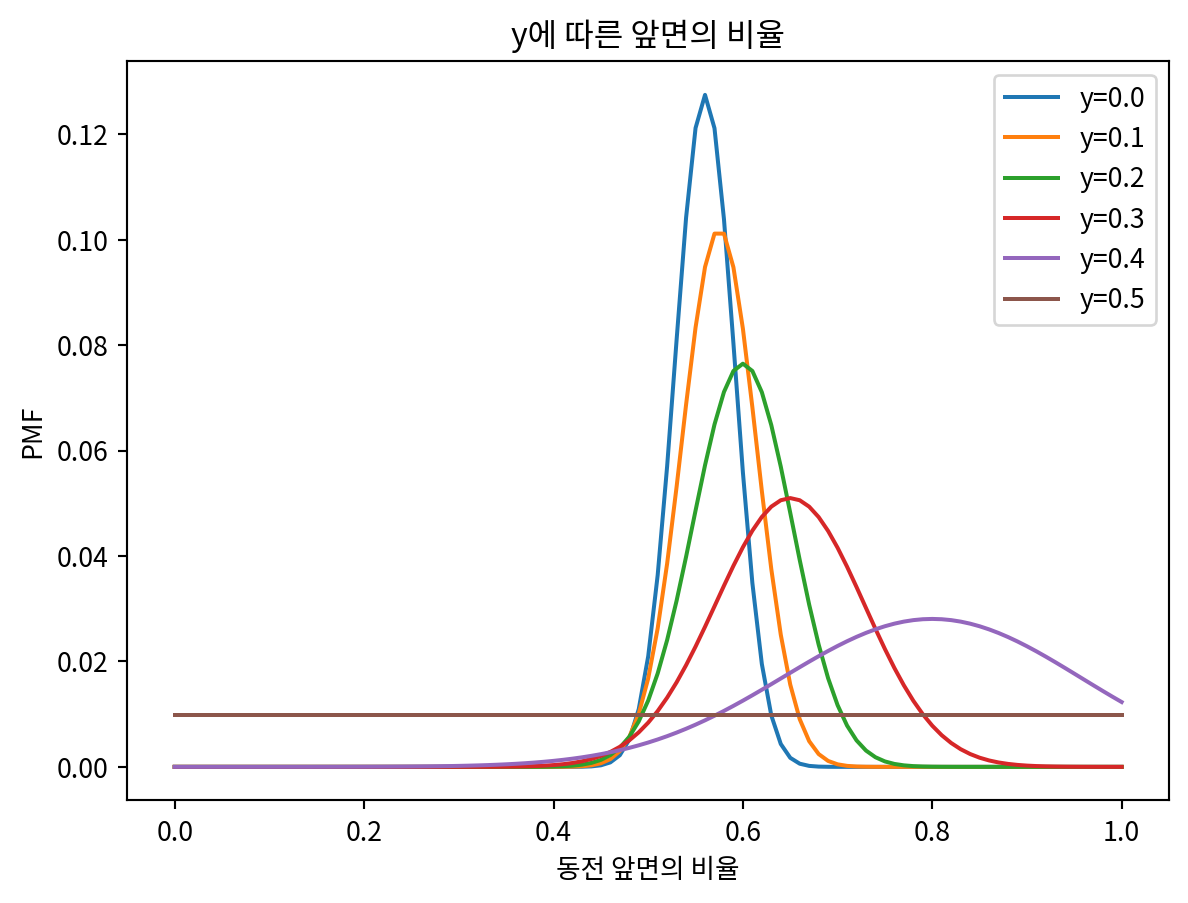
4-4
hypos = np.linspace(0.1, 0.4, 101)
uniform = Pmf(1, hypos)
prior = Pmf(1, hypos)
prior.normalize()
prob_both_0 = (1 - hypos) ** 4
prob_both_1 = (2 * hypos * (1 - hypos)) ** 2
prob_both_2 = hypos ** 4
likelihood = prob_both_0 + prob_both_1 + prob_both_2
posterior = uniform * likelihood
posterior.normalize()
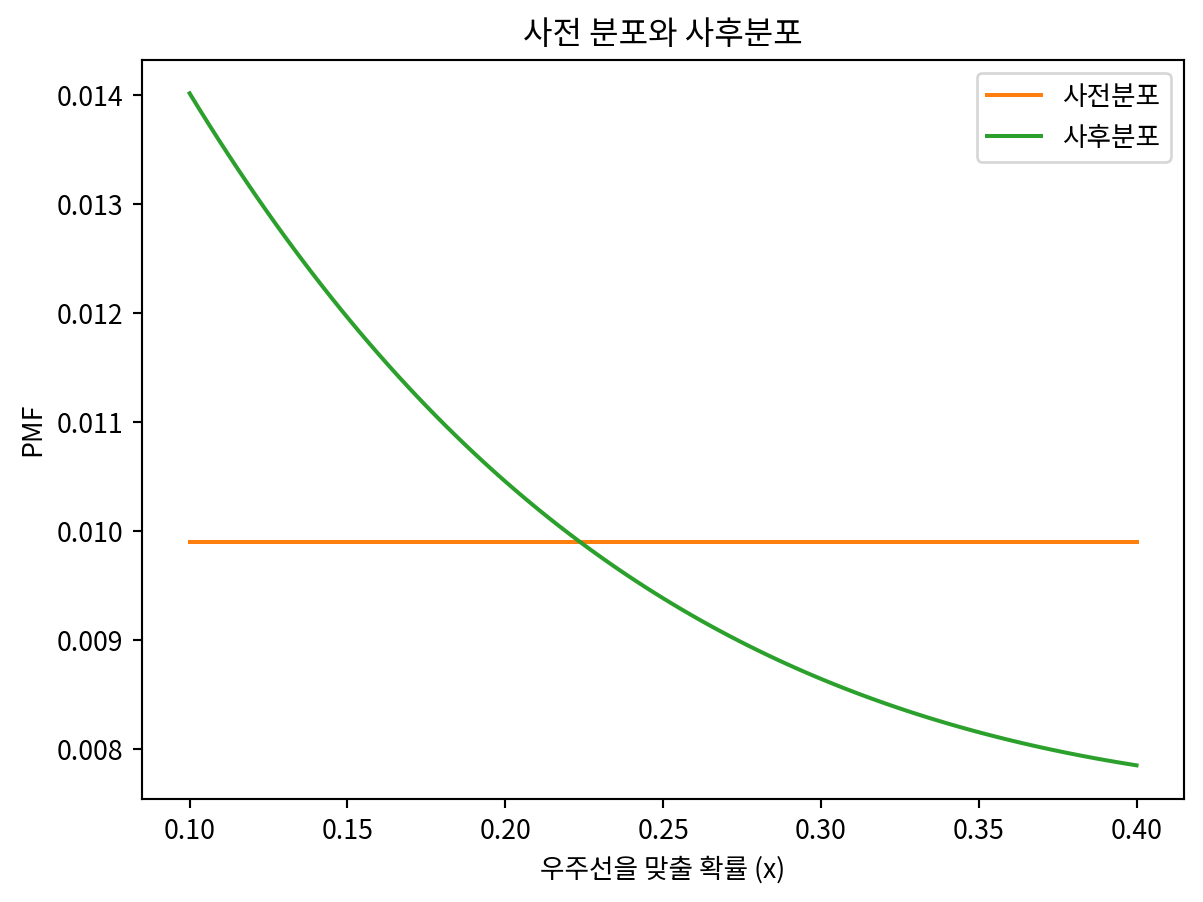
prior.plot(label='사전분포', color='C1')
posterior.plot(label='사후분포', color='C2')
plt.legend()
plt.title('사전 분포와 사후분포')
plt.xlabel('우주선을 맞출 확률 (x)')
plt.ylabel('PMF')
prior_mean = prior.mean()
posterior_mean = posterior.mean()
print("\n=== 연습문제 4-4 답변 ===")
if posterior_mean > prior_mean:
print("✅ 데이터는 좋은 소식입니다 (GOOD)")
print(f"✅ x의 추정값이 {prior_mean:.3f}에서 {posterior_mean:.3f}로 증가했습니다 (INCREASE)")
else:
print("❌ 데이터는 나쁜 소식입니다 (BAD)")
print(f"❌ x의 추정값이 {prior_mean:.3f}에서 {posterior_mean:.3f}로 감소했습니다 (DECREASE)")
=== 연습문제 4-4 답변 ===
❌ 데이터는 나쁜 소식입니다 (BAD)
❌ x의 추정값이 0.250에서 0.235로 감소했습니다 (DECREASE)