신뢰도 공학
품질경영

품질과 신뢰성
- 신뢰성: 시간적 측면에서 제품을 오랫동안 고장 없이 사용할 수 있는 것을 의미
- 관리도와의 차이점: 관리도는 특정 시점에서의 변동을 다룸(정적인 시간)
- 정해진 사용 조건 하에서 요구되는 기능을
주어진 기간동안 수행하는 능력
- 신뢰도: 시스템, 기기, 부품 등이 시간성 안정성을 나타내는 정도 (신뢰성의 정도)
- 신뢰성과 품질경영: 과거 품질 관리는 공정중심의 관리와 사후 관리에 치중되었으나, 신뢰도 공학은 사전예방 시스템으로 고장 발생 확률을 미리 예방하기 위해, 사전 시스템 공학적 품질경영을 추구
- 소비자가 사용하다가 고장이 나는 경우도 고려
신뢰도 공학의 특징
- 시스템 전 수명 주기에 걸친 체계적인 신뢰성 활동 요구
- 장기간 축적된 다양한 고유 기술들이 연관되어 있다.
- 신뢰성 데이터는 매우 고가
- 10년 수명 보장 제품을 만들려면 원칙적으로 10년 동안 테스트 해야 한다.
- 가속수명시험을 통계적으로 분석하여 10년 후를 예측. 하지만 과정이 복잡하고 비용이 크다.

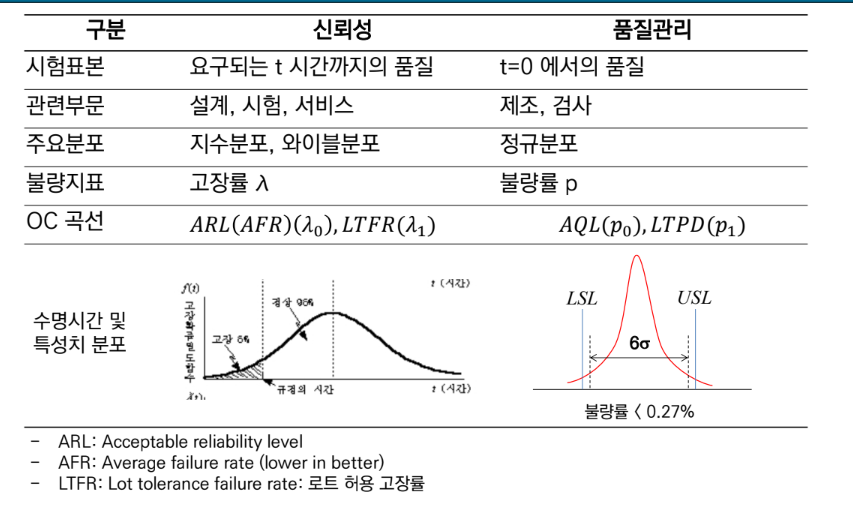
신뢰성 척도
- f(t): 특정 시점 t에서 시스템이 고장 날 확률의 밀도. 지수분포, 와이블 분포, 정규분포 등
- 신뢰도 함수 R(t): 제품이 t 시점까지 고장이 나지 않을 확률
- \(R(t) = P(T > t) = ∫[∞, t] f(x) dx\)
- 불신뢰도 함수 F(t): 제품이 t 시점 안에 고장이 날 확률
- F(t) = P(T ≤ t) = 1 - R(t)
- F′(t) = f(t)
- 고장률 함수 λ(t): 시점 t까지 생존한 제품이 아주 짧은 다음 시간 내에 고장 날 순간적인 비율
- \(λ(t) = \frac{f(t)}{R(t)} = \frac{f(t)}{1 - F(t)}\)
- \(R(t) = e^{-∫[0, t] λ(x) dx}\)
- \(f(t) = λ(t) e^{-∫[0, t] λ(x) dx}\)

욕조 곡선
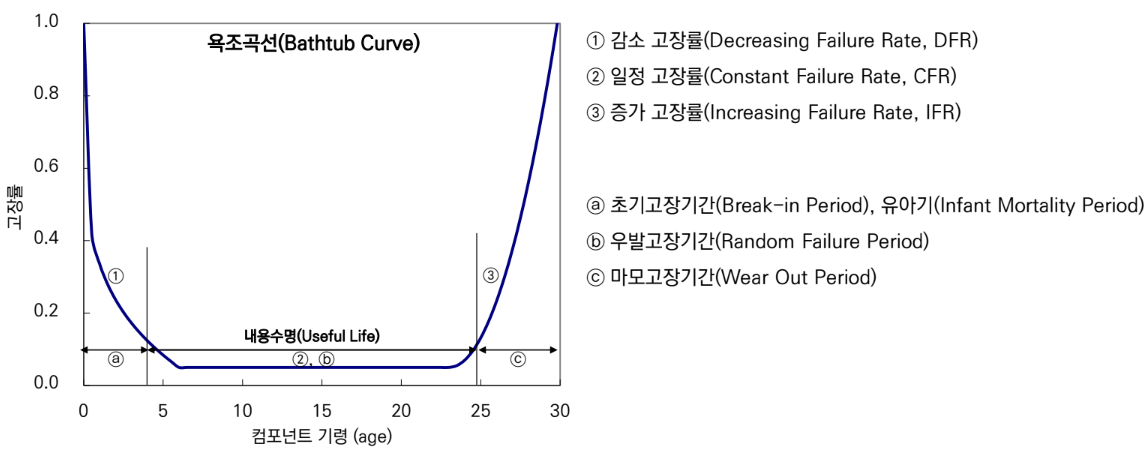
- 일반적으로 제조품의 고장률은 예방보전을 하지 않으면 욕조곡선을 그린다고 알려짐
- 수명 T가 Weibull 분포를 따른다고 가정
초기고장기간
- 사용 개시 후에 비교적 빠른 시간에 설계, 제조상의 결함 혹은 사용환경의 부적합으로 발생하는 고장
- 와이블 분포(α < 1)로 모델링
- 불량품들이 초기에 빠르게 걸러지면서 고장률이 급격히 감소
우발고장기간
- 안전계수(\(\frac{파괴강도(최대로 견딜 수 있는 힘)}{허용응력(실제하중)}\)) 여유있게 설정하면 고장률이 낮고 비교적 일정한 기간으로 유지된다.
- 와이블 분포(α = 1)로 모델링
마모고장기간
- 피로, 마모, 노화현상 등으로 고장률이 높아지는 기간
- 파국고장: 갑자기 기능을 잃어버림
- 열화고장: 점진적으로 부분적으로 기능을 상실함
- 적절한 예방보전으로 수명을 연장할 수 있음
- 정규분포 혹은 와이블 분포(α > 1)로 모델링
경험적 신뢰성 척도
- 실제 분포를 모를 때, 관측치만으로 신뢰성 척도를 추정하는 비모수적 방법


- 평균 순위법의 분모가 n+1인 이유는 안전장치를 둬서 샘플이 다 고장나도 아직 수명이 다 끝나지 않았다는 것을 고려
- 두 방식이 큰 차이는 없다
지수분포
- \(f(t) = λe^(-λt), t ≥ 0\)
- \(R(t) = e^(-λt)\)
- \(F(t) = 1 - e^(-λt)\)
- \(λ(t) = λ\) (t가 없다: 시간에 관계없이 고장률이 일정)
- 평균수명(MTTF): \(E(t) = 1/λ\)
정규분포
- 기계부품의 수명 분포에 활용
- \(f(t) = \frac{1}{σ}Φ(\frac{t - μ}{σ})\)
- \(R(t) = 1 - Φ(\frac{t - μ}{σ})\)
- 평균수명(MTTF): \(E(t) ~ μ\)(0부터 계산하니까 근사값. 하지만 거의 비슷함)
보전
- 고장나거나 결함이 있는 시스템을 수리를 통해 사용 가능한 상태로 유지하기 위한 조치 및 활동
- 사후 보전(BM): 고장날 때 까지 사용하고 고장나면 수리하는 것(고장보전, 대응보전)
- 예방 보전(PM): 고장을 예방하기 위해 고장 여부와 관계없이 주기적으로 점검, 수리, 교체하는 것(계획보전, 정기보전)
- 예측 보전(PdM): 실시간 데이터와 AI/통계 모델로 고장 징후를 미리 예측하고 고장이 임박했을 때 수리하는 방법
보전도
- M(t): 시스템이 고장났을 때, t 시간안에 수리가 끝날 확률을 의미
- Mean Time To Repair (MTTR): 평균 수리 시간
- MTTR이 1/μ일 때, 수리 시간이 지수분포를 따른다면
- \(M(t) = 1 - e^{-μt}\)
- 수리율: μ
가용도
- MTBF(Mean Time Between Failures): 평균 고장 간격 시간(MTTF + MTTR)
- 가용성 = MTTF / MTBF
- MTTR을 줄이는게 가용성 향상에 효율적
신뢰도 입증 시험
- 샘플이 목표 신뢰도 함수를 달성하는 지 검정
- 전수시험: 모든 대상의 수명을 관찰하는 시험
- 중단시험: 모두 수명을 다하기 전에 중단하는 시험
- 정시중단시험: 정해진 시간까지만 시험하고 중단(Type 1 censoring)
- 정수중단시험: 정해진 개수까지 고장나면 중단(Type 2 censoring)
지수 분포의 신뢰도 함수 추정

- 모수는 최우추정법으로 추정
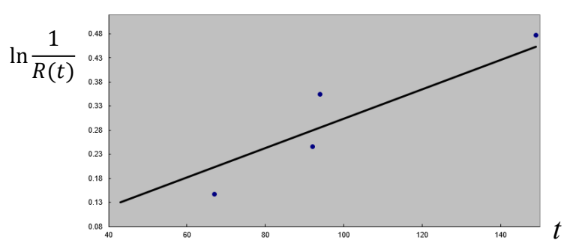
- \(R(t) = e^{-λt} -> \frac{1}{R(t)} = e^{λt} -> ln(\frac{1}{R(t)}) = λt\)
- median 순위법으로 R(t) 추정. 최우추정법으로 λ 추정
최우추정치의 신뢰구간

- r = 고장난 샘플 수
- 개수가 fix가 아니여서 정시중단 시험에 1개를 넣넣하게 넣어줌
- r = 0일 때: 정수중단시험은 계산 불가, 정시중단시험의 평균 추정치는 ∞, 신뢰구간은 \(-\frac{T}{lnα} ≤ θ ≤ ∞\)
- 수명이 지수분포를 따를 때, r은 포아송 분포를 따름
- \(P(r <= c) = ∑[0, c] e^{-m}m^r / r!\)
- 평균수명이 θ일 때, 총 시험시간(T) = \(n t_0\) 고장수의 평균 m = T / θ
- 무고장 확률 \(α = P(r = 0) = e^{-T/θ}\) (보통 0.05)로 설정
- 수명이 지수분포를 따를 때, r은 포아송 분포를 따름