분산 분석 템플릿

데이터 분석
공개

2025년 10월 5일

가정 검정

검정 방법 선택 기준

모수 검정 방법 선택 기준
  • 관측치 간에 독립이 아닌 경우(시간: 자기 상관이 존재, 공간: 패널, 계층, …), 각 케이스에 맞는 모형을 사용해야 함.

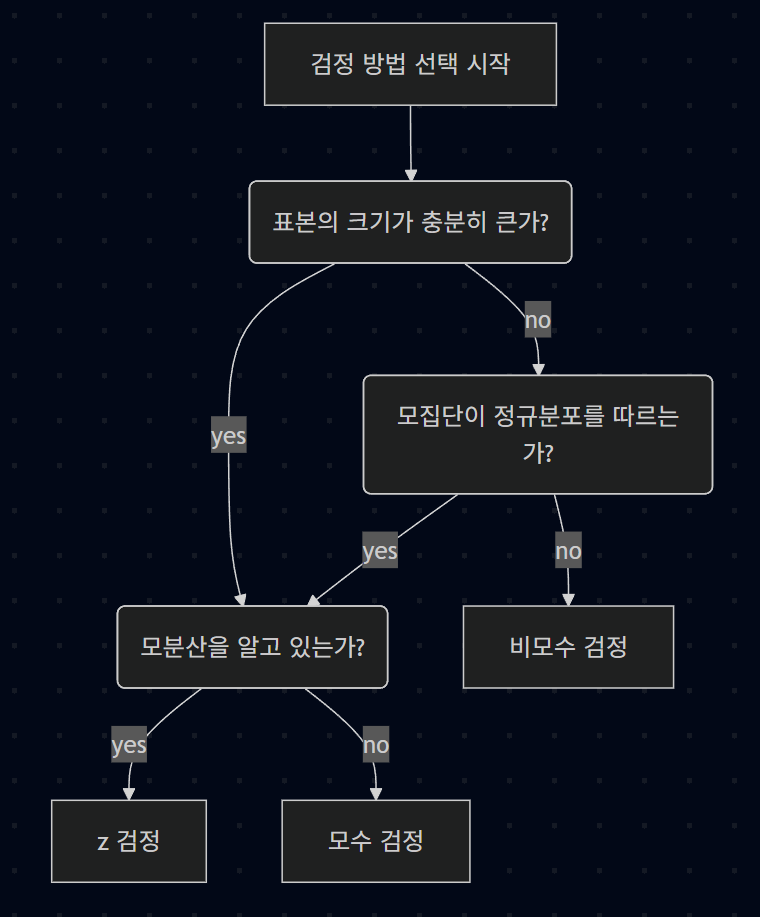
정규성 검정

  • 표본이 정규분포를 따르는지 검정.

  • 따르지 않더라도 중심극한정리에 의해 표본의 크기가 충분히 크면 모수 검정을 사용할 수 있다.

  • shapiro wilk 검정: 표본의 크기가 3-5000개인 데이터에 사용. 동일한 값이 많은 경우 성능이 떨어질 수 있음

    • H0: 데이터가 정규분포를 따른다.
    • H1: 데이터가 정규분포를 따르지 않는다.

  • jarque-Bera: 대표본에 사용.

    • H0: 데이터가 정규분포를 따른다.
    • H1: 데이터가 정규분포를 따르지 않는다.

  • Q-Q plot: x축이 이론적 분위수, y축이 표본 분위수

normality test
#| eval: false

from scipy.stats import shapiro, jarque_bera, zscore, probplot

data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
stat, p = shapiro(data)

print(f"Shapiro-Wilk Test: stat={stat:.3f}, p={p:.3f}")

stat, p = jarque_bera(data)
print(f"Jarque-Bera Test: stat={stat:.3f}, p={p:.3f}")

import matplotlib.pyplot as plt
import seaborn as sns

zdata = zscore(data)
fig, ax = plt.subplots(1, 2, figsize=(10, 3))

(osm, odr), (slope, intercept, r)) = probplot(zdata, plot=ax[0])
ax[0].set_title("Q-Q Plot")

sns.histplot(data, kde=True, ax=ax[1])
ax[1].set_title("Histogram")

plt.show()

등분산성 검정

  • Barlett 검정: 정규성을 만족하는 경우에만 사용 가능
    • H0: \(σ_1^2 = σ_2^2 = ... = σ_k^2\)
    • H1: \(σ_i ≠ σ_j\) for some i, j
  • Levene 검정: 정규성을 만족하지 않는 경우에도 사용 가능
    • H0: \(σ_1^2 = σ_2^2 = ... = σ_k^2\)
    • H1: \(σ_i ≠ σ_j\) for some i, j
equal variance test
#| eval: false

from scipy.stats import bartlett, levene

group1 = [1, 2, 3, 4, 5]
group2 = [2, 3, 4, 5, 6]
group3 = [3, 4, 5, 6, 7]

stat, p = bartlett(group1, group2, group3)
print(f"Bartlett's Test: stat={stat:.3f}, p={p:.3f}")

stat, p = levene(group1, group2, group3)
print(f"Levene's Test: stat={stat:.3f}, p={p:.3f}")

분산 분석

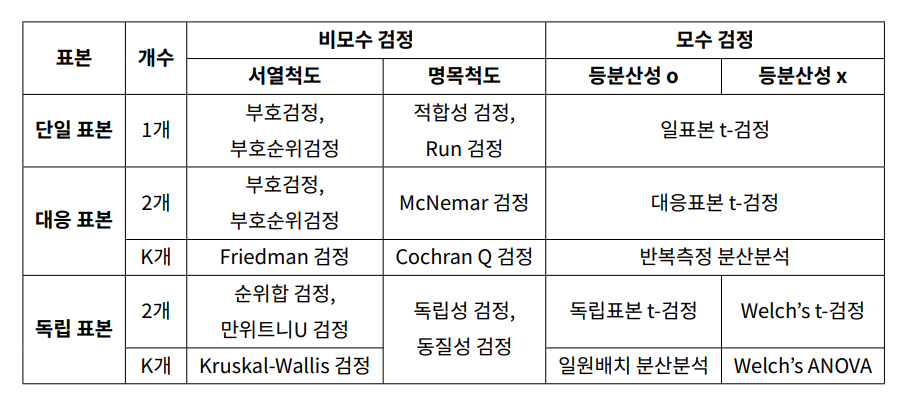
  • 정규성을 만족 못할 경우, 서열척도 비모수 검정 사용 가능
  • 코크란 Q 검정: 이항분포를 따르는 반복 측정 자료에 사용
    • 만약 대응표본이 아닐 경우 (실패, 성공) 변수를 만들어서 독립성 검정 사용
    • 만약 이항분포가 아닐 경우 프리드만 검정 고려
  • 독립성 검정의 cell의 기대도수가 5 미만인 경우, 피셔의 정확검정 사용
    • 만약 2x3을 넘어갈 경우 몬테카를로 시뮬레이션 사용(python으로 구현하기 복잡하다.)
  • 크루스칼, 맨휘트니: 동점이 과하게 많을 경우 permutation test, 순열 분산 분석 사용 가능
    • 하지만 ADP 환경의 scipy에서는 버전이 낮아서 permutation test를 쓸 수 없다.
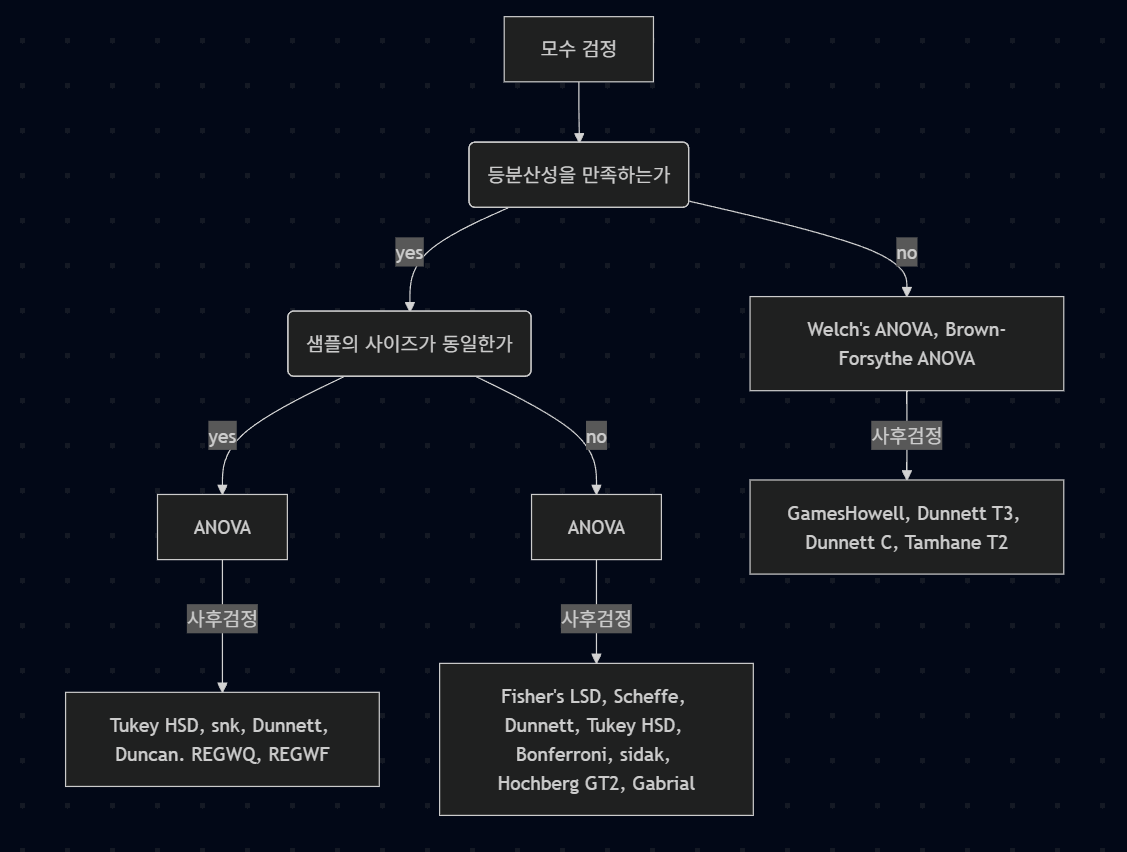
사후 검정
#| eval: false

from statsmodels.sandbox.stats.multicomp import MultiComparison
from scipy.stats import ttest_ind

mc = MultiComparison(data, groups).allpairtest(ttest_ind, method='bonf')
print(mc[0])

mc.plot_simultaneous()
plt.show()

적합성 검정

카이제곱 적합성 검정
#| eval: false

count = df_count['count'].value_counts().sort_index()

# 빈도 수가 5 미만인 경우 합침

count.loc[1] += count.loc[0]
count.loc[6] += count.loc[[7, 8]].sum()
count.drop([0, 7, 8], inplace=True)

# 모수 추정
lam = df_count['count'].mean()
poi = poisson(lam)

n = count.values.sum()
exp = np.array([(poi.pmf(0) + poi.pmf(1)), 
       *poi.pmf(np.arange(2, 6)), 
       poi.sf(5)]) # 마지막 값은 이상 값으로
exp *= n

from scipy.stats import chisquare

# 추정한 모수 갯수 만큼 자유도 차감
stat, p = chisquare(count.values, exp, ddof=1)
p
  • 연속형
    • 이표본 검정: 콜모고로프-스미르노프 검정 사용
    • 일표본 검정:
      • 정규분포, 지수분포: 앤더슨-달링 검정 사용
      • 그 외: 몬테카를로 방법 사용
  • 이산형
    • 이표본: 카이제곱 독립성 검정
    • 일표본: 카이제곱 동질성 검정

다변량 분산분석

2-way ANOVA

  • 반복이 없는 경우 교효작용 검정은 불가능
  • 정규성, 등분산성 검정은 잔차에 대해 수행
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm


model = ols("성적~C(성별)+C(교육방법)+C(성별):C(교육방법)", data=data).fit()
atab = anova_lm(model)
atab
from scipy.stats import shapiro

residuals = model.resid

shapiro_test = shapiro(residuals)
print(f"Shapiro-Wilk Test on Residuals: Statistic={shapiro_test.statistic}, p-value={shapiro_test.pvalue}")
sns.residplot(x=model.fittedvalues, y=residuals, lowess=True,
              line_kws={'color': 'red', 'lw': 2})
plt.show()
  • 교효작용이 유의하지 않을 경우 오차항에 pooling을 한다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm


model = ols("성적~C(성별)+C(교육방법)", data=tmp).fit()
atab = anova_lm(model)
atab
  • main 효과의 사후검정은 anova와 동일
    • 하지만 interation 효과가 유의할 경우, 주효과는 무의미하다.
  • interaction 효과는 시각적으로 보여주는게 좋다.
grouped = tmp.groupby(['성별', '교육방법'])['성적'].mean().reset_index()
pivot = grouped.pivot(index='성별', columns='교육방법', values='성적')
pivot.plot(marker='o')
plt.ylabel('평균 성적')
plt.title('성별-교육방법 교호작용 효과')
plt.legend(title='교육방법')
plt.tight_layout()
plt.show()
  • 2way 이상은 해석이 어려워서 잘 사용하지 않는다.

반복측정 분산분석

repeated measures anova
import pingouin as pg

df = pd.DataFrame({
    'subject': [1, 2, 3, 1, 2, 3, 1, 2, 3],
    'condition': ['T1', 'T1', 'T1', 'T2', 'T2', 'T2', 'T3', 'T3', 'T3'],
    'score': [80, 78, 85, 82, 80, 86, 88, 83, 90]
})

# 반복측정 ANOVA 수행 및 구형성 검정, 보정 포함
aov = pg.rm_anova(dv='score', within='condition', subject='subject', data=df, correction=True)
display(aov)
  • sphericity가 true이면 구형성 만족
  • p-unc: 구형성 보정 전 p-value
  • p-GG-corr: Greenhouse-Geisser 보정 후 p-value
    • 구형성 위반 시 사용
맨 위로