확률과 통계
데이터 분석
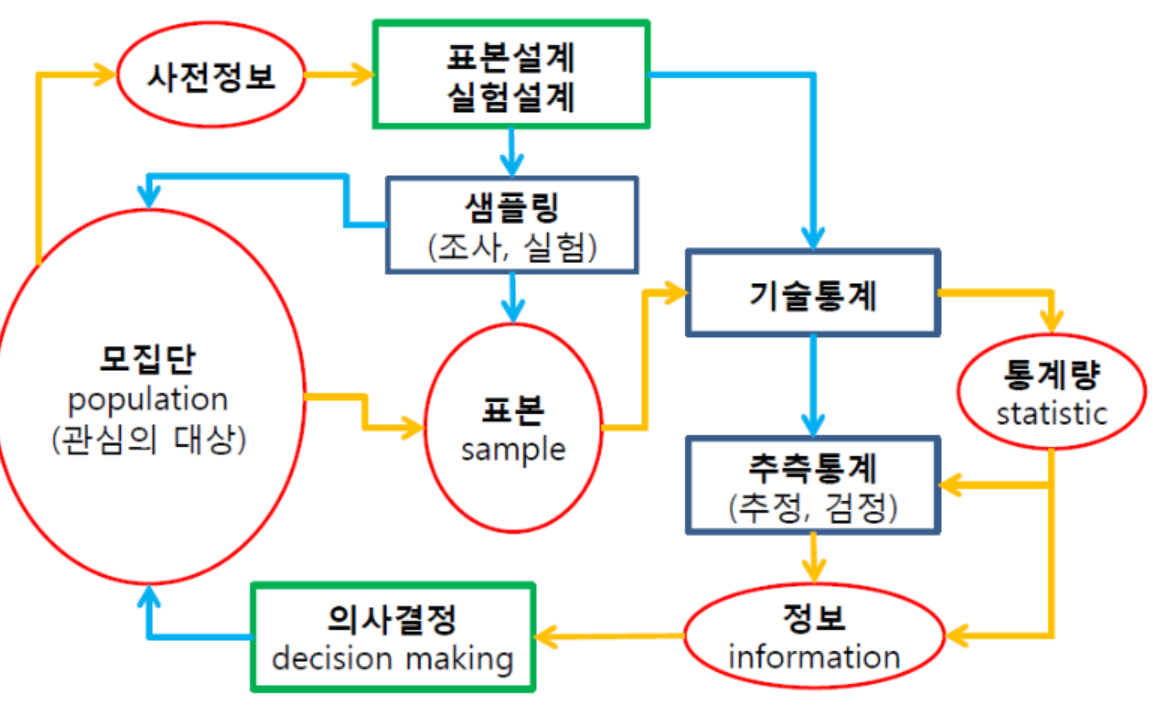
통계학
- 불확실한 상황 하에서 데이터에 근거하여 과학적인 의사결정을 도출하기 위한 이론과 방법의 체계
- 모집단으로 부터 수집된 데이터(sample)를 기반으로 모집단의 특성을 추론하는 것을 목표로 한다.
확률
- 고전적 의미: 표본공간에서 특정 사건이 차지하는 비율
- 통계적 의미: 특정 사건이 발생하는 상대도수의 극한
- 각 원소의 발생 가능성이 동일하지 않아도 무한한 반복을 통해 수렴하는 값을 구할 수 있다.
확률 분포 정의 단계
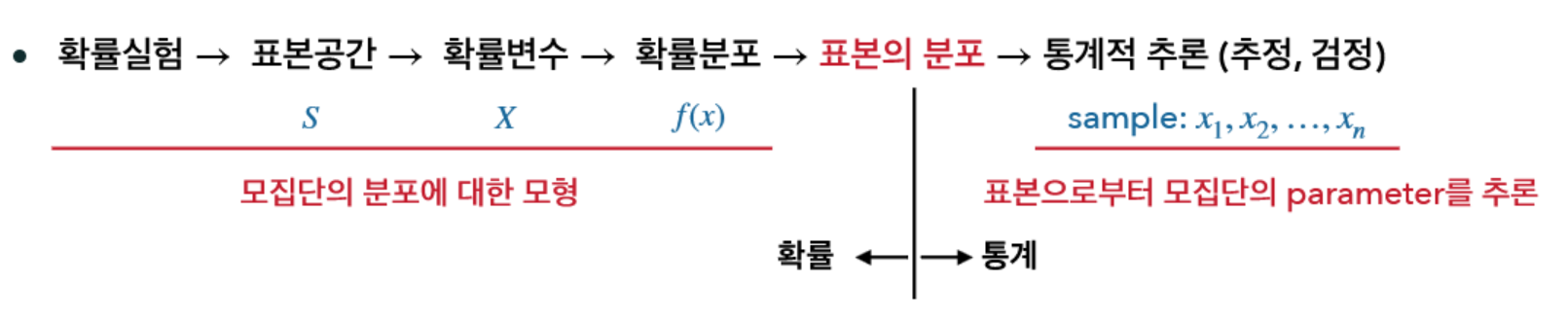
- Experiment(확률실험): 동일한 조건에서 독립적으로 반복할 수 있는 실험이나 관측
- Sample space(표본공간): 모든 simple event의 집합
- Event(사건): 실험에서 발생하는 결과 (부분 집합)
- Simple event(단순사건): 원소가 하나인 사건
- 확률 변수: 확률실험의 결과를 수치로 나타낸 변수
확률 분포
이산 확률 분포
이산 표본 공간, 연속 표본공간에서 정의 가능포
- 베르누이 시행: 각 시행은 서로 독립적이고, 실패와 성공 두 가지 결과만 존재.
- 단 모집단의 크기가 충분히 크고, 표본(시행)의 크기가 충분히 작다면 비복원 추출에서도 유효
- 평균: p
- 분산: p(1-p)
- 이항 분포: n번의 독립적인 베르누이 시행을 수행하여 성공 횟수를 측정
- X ~ B(n, p), \(f(x) = \binom{n}{x} p^x (1-p)^{n-x}\)
- 평균: np
- 분산: np(1-p)
- n이 매우 크고, p가 매우 작을 때, 포아송 분포로 근사할 수 있다. (λ = np)
- 음이항 분포
- 정의: n번의 독립적인 베르누이 시행을 수행하여 k번 성공하고, r번 실패한 경우 (n = k + r)
- r번의 실패가 나오기 전까지, 성공한 횟수 x
- X ~ NB(r, p), \(f(x) = \binom{x+r-1}{x} p^x (1-p)^r\)
- 평균: \(\frac{rp}{1-p}\)
- 분산: \(\frac{rp}{(1-p)^2}\)
- r번의 실패가 나오기 전까지, 시행한 횟수 x
- 4번에서 성공을 실패로 바꿈
- k번의 성공이 나오기 전까지, 실패한 횟수 x
- 1번에서 실패를 성공으로 바꿈
- k번의 성공이 나오기 전까지, 시행한 횟수 x
- \(f(x) = \binom{x-1}{k-1} p^k (1-p)^{x-k}\)
- k가 1일 때 기하분포와 동일
- n번의 시행 횟수에서, k번 성공 또는 r번 실패한 경우: 이항분포
- r번의 실패가 나오기 전까지, 성공한 횟수 x
- 정의: n번의 독립적인 베르누이 시행을 수행하여 k번 성공하고, r번 실패한 경우 (n = k + r)
- 기하 분포:
- 정의:
- 성공 확률이 p인 베르누이 시행에서 첫 성공까지의 시행 횟수
- X ~ G(p), \(f(x) = (1-p)^{x-1} p, x = 1, 2, 3, ...\)
- 평균: \(\frac{1}{p}\)
- 분산: \(\frac{1-p}{p^2}\)
- 성공 확률이 p인 베르누이 시행에서 첫 성공까지의 실패 횟수
- X ~ G(p), \(f(x) = (1-p)^x p, x = 0, 1, 2, ...\)
- 평균: \(\frac{1-p}{p}\)
- 분산: \(\frac{1-p}{p^2}\)
- 성공 확률이 p인 베르누이 시행에서 첫 성공까지의 시행 횟수
- 비기억 특성: \(P(X > n+k | X > n) = P(X > k)\)
- 정의:
- 초기하 분포: 베르누이 시행이 아닌 시행에서 성공하는 횟수
- X ~ H(n, N, k), \(f(x) = \frac{\binom{K}{x} \binom{N-K}{n-x}}{\binom{N}{n}}\)
- 평균: \(\frac{nK}{N}\)
- 분산: \(\frac{nK(N-K)(N-n)}{N^2(N-1)}\)
- 포아송 분포: 임의의 기간동안 어떤 사건이 간헐적으로 발생할 때, 동일한 길이의 기간동안 실제 사건이 발생하는 횟수
- X ~ Poisson(λ), \(f(x) = \frac{e^{-λ} λ^x}{x!}, λ > 0\)
- 평균: λ
- 분산: λ
연속 확률 분포
연속 표본 공간에서 정의 가능
- 균일 분포
- \(f(x) = \frac{1}{b-a}, a ≤ x ≤ b\)
- 평균: \(\frac{a+b}{2}\)
- 분산: \(\frac{(b-a)^2}{12}\)
- 정규 분포
- \(X + Y \sim N(μ_1 + μ_2, σ_1^2 + σ_2^2)\)
- 선형 변환: \(Y = aX + b \sim N(aμ + b, a^2σ^2)\)
- t 분포
- 자유도가 커질수록 표준 정규분포에 근사함.
- \(\frac{Z}{\sqrt{V/n}} \sim t(n)\), Z: 표준정규분포, V: 자유도가 n인 카이제곱분포
- f 분포
- \(F = \frac{X_1/ν_1}{X_2/ν_2}\), \(X_1 \sim χ^2(ν_1)\), \(X_2 \sim χ^2(ν_2)\), X1과 X2는 서로 독립
- 감마 분포
- α: 분포의 형태 결정, θ: 분포의 크기 결정
- 평균: αθ
- 분산: αθ²
- 카이제곱 분포: α = v/2, θ = 2 인 감마분포
- \(Z_i \sim N(0,1)\)일 때, \(Z_1^2 + Z_2^2 + ... + Z_n^2 \sim χ^2(n)\)
- \(X_i\)가 서로 독립이고, 자유도가 \(ν_i\)인 카이제곱분포를 따른다면, \(X_1 + X_2 + ... + X_n \sim x^2(ν_1 + ν_2 + ... + ν_n)\)
- 자유도가 커질수록 기댓값을 중심으로 모이고, 대칭에 가까워진다.
- 지수 분포: α = 1, θ = 1/λ 인 감마분포
- \(X ~ Exp(λ = \frac{1}{θ})\), f(x) = \(λe^{-λx}, x > 0\)
- θ: 평균 사건 발생 간격, λ: 단위 시간당 사건 발생 횟수
- 포아송 분포에서 사건 발생 간격의 분포
- \(\sum_{i=1}^{n} X_i \sim Γ(n, θ)\), \(θ = 1/λ\)
- 비기억 특성을 가진다: \(p(X > s + t | X > s) = p(X > t) = e^{-λt}\)
- 독립적으로 동일한 지수분포를 따르는 확률변수 n개의 합은 \(α = n, θ = \frac{1}{λ}\)인 감마분포를 따른다.
다변량 분포
- 다항 분포: n번의 독립적인 베르누이 시행을 수행하여 k개의 범주로 분류
- X ~ M(n, p1, p2, …, pk), \(f(x_1, x_2, ..., x_k) = \frac{n!}{x_1! x_2! ... x_k!} p_1^{x_1} p_2^{x_2} ... p_k^{x_k}\)
- 평균: \([np_1, np_2, ..., np_k]\)
- 분산: \([np_1(1-p_1), np_2(1-p_2), ..., np_k(1-p_k)]\)
- 공분산: \(-np_ip_j (i ≠ j)\)
- 독립인 변수의 갯수는 k-1개 (k개의 사건)
샘플링
분포의 동질성 검정
- 연속형
- 이표본 검정: 콜모고로프-스미르노프 검정 사용
- 일표본 검정:
- 정규분포, 지수분포: 앤더슨-달링 검정 사용
- 그 외: 몬테카를로 방법 사용
- 이산형
- 이표본: 카이제곱 독립성 검정
- 일표본: 카이제곱 동질성 검정
표본의 분포
샘플링에 따라 통계량이 다른 값을 가질 수 있다. 따라서 통계량의 분포를 이용한 통계적 추론이 가능하다.
통계량: 표본의 특성을 나타내는 값
추정량: 아래의 조건을 만족하는 통계량
- 불편성: 추정량의 기대값이 추정하려는 모수와 같아야 한다.
- 효율성: 분산이 작아야 한다. 표본의 갯수가 많아질수록 분산이 작아져야 한다.
표본 평균의 분포
- 모집단의 분포와 관계없이, 모집단의 평균이 μ이고, 분산이 \(σ^2\)이면, \(\bar{X}\)의 평균은 μ이고, 분산은 \(σ^2/n\)인 정규분포를 따른다.
- 단 모집단의 분포에 따라 표본의 크기가 충분히 커야함. (중심극한정리1)
- 만약 모집단의 분산을 모를 경우, σ를 s로 대체하여, t분포를 따르는 표본 평균의 분포를 구할 수 있다.
- 단 이때는 모집단이 정규분포를 따라야 한다.
표본 분산의 분포
- 정규 모집단으로 부터 나온 표본의 분산 S에 대하여, \(\frac{(n-1)S^2}{σ^2}\)은 자유도가 n-1인 카이제곱 분포를 따른다.
- 모집단이 정규분포를 따르지 않을 경우, 비모수적인 방법을 사용해야 한다.
- 두 정규 모집단으로부터 계산되는 표본분산의 비율은 f-분포를 따른다.
추정
- 통계적 추론: 모집단에서 추출된 표본의 통계량으로부터 모수를 추론하는 것
- 추정
- 점추정
- 구간추정
- 가설 검정
- 추정
점 추정
- 불편성
- \(E(\hat{\theta}) = θ\)
- bias = \(E(\hat{\theta}) - \theta\)
- 보통 sample size가 커질수록 bias는 0에 수렴
- \(\bar{X}, X_n\)은 μ의 불편추정량이다.
- 최소분산
- \(Var(\bar{X})\)가 \(Var(X_n)\)보다 분산이 작아서 더 좋은 추정량
- \(MSE(\hat{\theta}) = E[(\hat{\theta} - \theta)^2] = Var(\hat{\theta}) + bias^2\)
- 큰 오차에 더 큰 페널티를 주기 위해 제곱

- 전부 중심극한의정리를 적용할 수 있다. (비율은 0과 1의 평균이므로)
- 모평균, 모비율의 차이는 서로 독립이라는 가정이 필요하다.
구간 추정
- α: 유의수준
- 1 - α: 신뢰수준2
- (θ_L, θ_U) = (1 - α) × 100% 신뢰구간
- (\(θ_L, θ_U\)) 이 충분이 높은 가능성으로 미지의 모수 θ를 포함해야 한다
- 구간이 충분히 좁아야 한다
- 표준 정규분포에서 0을 중심으로 대칭일 때 길이가 짧다.
- 고로 신뢰구간이 대칭임
표본의 크기 결정
특정 오차 아래로 하는 표본의 수 구하는 법
- 그냥 표본오차가 목표 오차보다 작게 하는 값을 구하면 됨.
- 모비율을 모를 때는 일단 0.5로 보수적으로 놓고 계산
모분산 추정
- 카이제곱 분포는 가장 짧은 신뢰구간을 구하기 쉽지 않음
- 그냥 쉽게 구하기 위해 \((x^2_{α/2}, x^2_{1-α/2})\)를 사용
- 모분산의 신뢰구간: \((\frac{(n-1)s^2}{x^2_{(1-\alpha)/2}(n-1)}, \frac{(n-1)s^2}{x^2_{\alpha/2}(n-1)})\)
- 표본의 수가 적을수록, 카이제곱 분포의 신뢰구간은 더 길어진다.